Lekcija v 6. razredu na temo:
"Izdelek celih števil"
Cilji:
Izpeljite pravila za množenje celih števil.
... Oblikovati poznavanje pravil za množenje pozitivnih in negativne številke in sposobnost njihove uporabe v najpreprostejših primerih.
Naučiti se uporabljati ta pravila v najpreprostejših situacijah.
Naučiti se določiti stopnjo celih števil z naravnim eksponentom.
Razviti sposobnost primerjanja, ugotavljanja vzorcev, posploševanja.
Vzgajati odgovoren odnos do dela.
oprema:
Interaktivna tabla (projektor z zaslonom), kartice z nalogami za vsakega učenca.
Struktura lekcije:
Revitalizacija učne dejavnosti
Postavitev cilja lekcije.
Učenje nove snovi.
Uprizoritev Domača naloga.
Obnašanje rezultata (refleksija).
Med poukom:
Ponavljanje predhodno naučene snovi.
Še naprej preučujemo pozitivne in negativne številke ter dejanja nanje.
2. diapozitiv:
Geslo naše lekcije»Znanje je najboljša lastnina. Vsi si prizadevajo za to, a sama ne pride." Al-Beruni
Frontalna anketa (slajd 3.4)
Intenziviranje izobraževalnih dejavnosti (slajd 5.6)
Preverjanje opravljenega dela (diapozitiv 7).
Priprava na učenje nove snovi.
Ustvarjanje problemske situacije (slajd 8).
Postavitev cilja lekcije (prosojnica 9).
Učenje novega gradiva (slajd 10, 11, 12, 13, 14)
Z učenci se pogovorite o dobljenih rezultatih, primerjajte in ugotovite vzorce pri določanju predznaka dela in njegovega modula.
Oblikujemo pravila za množenje dveh števil z različni znaki in dve negativni števili.
Odvisnost, povezana s spremembo predznaka dela, ko se spremeni predznak enega od dejavnikov. Na glas preberemo pravila za množenje dveh števil z različnimi predznaki in dveh negativnih števil. Opozarjamo na dejstvo, da je zmnožek negativnih števil pozitivno število, zmnožek števil z različnimi predpisi pa negativno število.
Razumevanje in uporaba naučenega.
Diapozitiv 15, 16.
Ustno rešimo: 6 x (-3) 6 x (-1) (-5) x (-1) (-5) x 7 6 x (-1) 6 x 2 (-5) x 0 (-5) x (-3).
Povemo v celoti: zmnožek šest in minus tri je enak minus osemnajst, saj pri množenju števil z različnimi predznaki dobimo negativno število, njegov modul pa je enak zmnožku modulov faktorjev.
Naslednja naloga to naredimo pisno in tudi izgovorimo.
Pisno delo (slajd 17)
Vsak učenec se izmenično ob tabli reši 2 primera.
Telesna vzgoja (slajd 18).
Samostojno delo(delo v parih), sledi medsebojno preverjanje in podajanje predhodnih ocen (diapozitiv 19, 20, 21).
Delo z učbenikom (22. diapozitiv).
Sami preberite testni odlomek učbenika, se z učenci pogovorite o prebranem gradivu in rešite primere, prikazane na diapozitivu. Vsak učenec ustno ali na tabli reši 2 primera.
Reševanje nalog o uporabi pravil za množenje celih števil (slajd 23, 24, 25, 26).
5. Postavljanje domače naloge
(slajd 27)
Naučite se teoretičnega gradiva na strani 2.7.
Reši št. 310, št. 121 (RT)
Pomislite na pravila za deljenje celih števil (namig: obratno dejanje za deljenje je množenje)
Študentom je dana možnost, da se seznanijo z vsebino domače naloge in dobijo potrebne nasvete.
Povzetek lekcije (razmislek)
Diapozitiv 28, 29, 30.
Vsakemu učencu omogočite, da na kratko spregovori, tako da odgovori na vprašanja na diapozitivu in samoanalizira svoje dejavnosti. Tako lahko ocenite učinkovitost asimilacije učno gradivo, označite študente.
Bibliografija:
matematika. 6. razred: učbenik za splošno izobraževanje. institucije / S. M. Nikolsky, M. K. Potapov, N. N. Reshetnikov, A. V. Shevkin. - M .: Izobraževanje, 2014;
matematika. 6. razred: didaktično gradivo / M.K. Potapov, A.V. Shevkin. - M .: Izobraževanje, 2014.
Delovni zvezek o matematiki za 6. razred M. K. Potapov, A. V. Shevkin. - M .: Izobraževanje, 2014.
matematika. Tematski testi. 6. razred: priročnik za učitelje splošne vzgoje. organizacije / P.V. Chulkov, E.F. Shershnev, O.F. Praska. - M .: Izobraževanje, 2014.
Namen lekcije:
Vzgojno: razvijanje spretnosti množenja celih števil z različnimi predznaki.
Vzgojna: gojenje kulture vzgojno-izobraževalnega dela in zanimanja za predmet.
Razvoj:
- Razvoj kognitivnega zanimanja;
- Razvoj sposobnosti analiziranja, primerjanja, gradnje analogij;
- razvoj logično razmišljanje, spomin, pozornost;
- Razvoj matematičnega govora.
Oprema za pouk:
- Karte za iskanje;
- ilustracije:
- Pravila za množenje celih števil (slika 1);
- Pravilo predznakov pri množenju celih števil (slika 2).
MED POUKOM
Organiziranje časa.
Učitelj: Pozdravljeni fantje, sedite. Danes v lekciji vas želim prositi za pomoč. Dejstvo je, da sem dobil nalogo: zelo lepo urediti obrazce za odgovore glede na podane primere. Upam, da mi lahko pomagate pri tem. Vsak od njih ima na mizi list z nalogo in polje za odgovore. Prosim vas, da ste pri odločanju in zapisovanju rezultatov teh dejanj zelo previdni. Številke nalog ustrezajo številkam odgovorov. Vsako številko dobljene digitalne rešitve zapišemo v ločeno polje, od leve proti desni (pokaže vzorec izpolnjevanja polja za odgovore). Ali vsi razumejo? Rešitev primerov bomo zapisali v zvezek za razredno delo.
Priprava na učenje nove snovi.
Preden začnemo s to nalogo, poglejmo, katera pravila moramo uporabiti.
Učenci: Pravila za seštevanje celih števil.
Učitelj: Bravo!
1) Katera števila se imenujejo cela števila?
2) Kakšen je modul števila?
3) Kako sešteti številke z enakimi predpisi?
4) Kako sešteti številke z različnimi predpisi?
Dobro opravljeno! Pojdimo torej k rešitvi. Odprli so delovne zvezke, zapisali številko na rob.
Učenca pokličejo na tablo, da izvede rešitev z razlago. Rešimo jo po vrsti in jo takoj zapišemo v polje za odgovor.
Učenci rešujejo naloge.
Učitelj: Ja, bojim se, da tudi pri vas ne bomo imeli časa, da bi med poukom vse uredili. Mogoče lahko nekako pospešite proces računanja?
Učenci: Da, dejanje seštevanja lahko zamenjate z - množenjem.
Oblikovanje teme lekcije.
Učitelj: Bravo! To bo tema naše lekcije. Zapisali smo ga v zvezek »Množenje celih števil«. In danes ti in jaz ne bomo samo množili naravnih števil, ampak se bomo tudi naučili množiti negativna cela števila in števila z različnimi predznaki.
Asimilacija novega znanja.
Z reševanjem primerov nadaljujemo tako, da nalogo zapišemo z dejanjem množenja
4) 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 8 7 = 56
Učitelj: Oglejte si naslednji primer v svojih nalogah (-3 + (- 3) + (- 3) =). Kako se ta primer razlikuje od tistega, ki ste ga pravkar rešili?
Učenci: Glede na vsoto treh enakih negativnih števil.
Učitelj: Ali lahko ta znesek zapišemo z dejanjem množenja?
Učenci: Da.
Učitelj: Kako?
5) -3 + (- 3) + (- 3) = -3 3 = - 9.
6) -6 + (- 6) + (- 6) + (- 6) + (- 6) + (- 6) = 6 (-6) (posneto)
Učitelj: Ali bi to množenje lahko zapisali kot (-6) 6?
Študentje: Da
Učitelj: Kako se imenuje zakon, ki nam omogoča, da zamenjamo množitelje?
Učenci: Potovanje.
Učitelj: Bravo! In tako, vsi primeri so rešeni, polja za odgovore so izpolnjena. Hvala za pomoč! Prosim izročite obrazce.
Učitelj: Še naprej bomo delali na temo "Množenje celih števil".
Fantje, poglejte, katera števila z znakom smo pomnožili v prvih štirih primerih?
Učenci: Oba sta pozitivna.
Učitelj: In kakšen je bil znak rezultata?
Učenci: Pozitivno.
Učitelj: In v primerih 5 in 6, katere številke so vključene v dejanje glede na znak?
Študentje: pozitivni in negativni.
Učitelj: In rezultat?
Študentje: Negativno.
Učitelj: Ali lahko oblikujemo pravilo za množenje pozitivnih števil?
Učenci: Ja! (formuliraj)
Učitelj: In množenje števil z različnimi znaki?
Učenci: Ja! (formuliraj)
Učitelj: Bravo! In množenje katerih številk še nismo upoštevali?
Učenci: Dva negativna.
Učitelj: Seveda, poskusimo uganiti rezultat.
En učenec dela za tablo.
Učitelj: Zakaj? Kako ste uganili?
Učenci: Pravilo razširitve oklepaja.
Učitelj: Bravo! Torej, "Pravilo za množenje celih števil". Zapišimo (pokaže ilustracijo in pove pravilo)
A * (-b) = - | a | * | b |
A * (+ b) = - | a | * | b |
A * (+ b) = + | a | * | b |
A * (- b) = + | a | * | b |
slika 1
Zapišimo tudi ločeno tabelo znakov za zmnožek dveh celih števil (prikazuje ilustracijo)
riž. 2
Učitelj: Poslušajte, kako so starodavni matematiki razlagali ta pravila:
Pravila za množenje, deljenje, seštevanje in odštevanje je v 3. stoletju predlagal grški matematik Diofant. Zvenele so nekako takole: "odšteti, pomnoži z dodanim, da odšteto," odšteje, pomnoži z odštetim, da dodano "
V 7. stoletju je indijski matematik Bramagupta pravila seštevanja in odštevanja negativnih števil izrazil takole: »vsota dveh sredstev je lastnina«, »vsota dveh dolgov je dolg«.
O predznaku rezultata, ki ga dobimo z množenjem dveh števil, ki ni nič, je znano tudi naslednje pravilo starodavnih:
prijatelj mojega prijatelja je moj prijatelj (+) (+) = (+)
prijatelj mojega sovražnika je moj sovražnik (+) (-) = (-)
sovražnik mojega prijatelja je moj sovražnik (-) (+) = (-)
sovražnik mojega sovražnika je moj prijatelj (-) (-) = (+)
Minuto počitka.
Učitelj: Utrujen? Odpočijmo si od matematike, delajmo matematiko!
1 naloga:
Dokončaj povedi:
3 prijateljem dolgujem po 5 rubljev. Moj: .
Izgubil sem 7 tekem za 4 točke. Moj račun:
2. naloga:
Na ta vprašanja je treba hitro odgovoriti:
Koliko repov ima sedem mačk?
Koliko prstov imajo štirje fantje?
Koliko ušes imajo tri starke?
Koliko ušes ima pet dojenčkov?
Koliko repov ima sedem psov?
Koliko glavnikov ima pet petelinov?
Preizkušanje učenčevega razumevanja nove snovi.
Učitelj: Fantje, danes ste me tolikokrat presenetili, znova me presenetite. (Učenca pokličejo k tabli, ostali delajo v zvezkih).
Izvedite dejanja (narek)
4) (-10+3)*(1-9)=
Učitelj: Bravo! In zdaj štafeta. Kdo hitro? Fantje proti puncam!
Pravila: reši primer in s seznama izberi črko s številko prejetega odgovora. Naprej!
(Primeri za rešitev so vnaprej napisani na skritem delu table v stolpcu, učenci le zapišejo odgovor. Črke s številkami so enako vnaprej zapisane.)
| Naloge za fante | Naloge za dekleta |
| 4*(-20)= -80 | 7*(-8)= -56 |
| -15*5= -75 | -40*2= -80 |
| 10 *(-10)= -100 | 13*3= 39 |
| 25*(-3)= - 75 | -4*(-7)= 28 |
| -6*(-11)= 66 | -2*(-24)= 48 |
| 4*12= 48 | 5*8= 40 |
| -20*(-2)= 40 | -15*(-4)= 60 |
C I M N L O U Y D
48 28 60 -80 39 -100 -75 -56 40 66
Povzetek:
Učitelj: Bravo in pametno!
Torej, fantje, kaj ste se novega naučili v lekciji danes?
Učenci: Spoznali smo, kako se množijo negativna cela števila in števila z nasprotnimi predznaki.
Učitelj: V naslednji lekciji se bomo še naprej ukvarjali s to temo in se naučili še veliko zanimivih stvari.
Informacije za učence o domačih nalogah.
V zvezke zapišite svojo domačo nalogo: sestavite križanko na podlagi definicij in pravil teme »Cela števila« in »dejanja seštevanja, odštevanja in množenja celih števil«.
V dnevnikih: Vpisi pravil v zvezek. št. 289, št. 296 po učbeniku Nikolskega "Matematika".
Hvala za vadnico in še enkrat hvala za pomoč.
Pri množenju in deljenju celih števil velja več pravil. V tej vadnici bomo obravnavali vsakega od njih.
Pri množenju in deljenju celih števil bodite pozorni na znake števil. Od njih bo odvisno, katero pravilo uporabiti. Prav tako je treba preučiti več zakonov množenja in deljenja. Učenje teh pravil se izogne nekaterim nadležnim napakam v prihodnosti.
Vsebina lekcijeZakoni množenja
V lekciji smo preučili nekaj zakonov matematike. Vendar nismo upoštevali vseh zakonov. V matematiki je veliko zakonov in bi bilo pametneje, da bi jih po potrebi preučevali zaporedno.
Najprej se spomnimo, iz česa je sestavljeno množenje. Množenje je sestavljeno iz treh parametrov: množljiv, množitelj in deluje
Tukaj je 3 množitelj, 2 je množitelj, 6 je produkt.
Množenec kaže, kaj točno povečujemo. V našem primeru povečamo število 3.
Faktor prikazuje, kolikokrat je treba povečati množitelj. V našem primeru je množitelj število 2. Ta množitelj prikazuje, kolikokrat morate povečati množitelj 3. To pomeni, da se bo med operacijo množenja število 3 podvojilo.
Delo - to je dejanski rezultat operacije množenja. V našem primeru je produkt številka 6. Ta izdelek je zmnožek 3 krat 2.
Izraz 3 × 2 lahko razumemo tudi kot vsoto dveh trojk. Množitelj 2 in v tem primeru bo pokazal, kolikokrat je treba dodati trojke:

Transpozicijski zakon množenja
V lekciji smo že obravnavali premični zakon množenja. Ponovimo še enkrat.
Množitelj in množitelj se imenujeta z eno skupno besedo - dejavniki... Transpozicijski zakon množenja je naslednji:
Izdelek se ne spremeni zaradi prerazporeditve mest dejavnikov.
Preverimo, če je temu tako. Pomnožimo na primer 3 s 5. Tukaj sta 3 in 5 faktorja.
Zdaj pa zamenjajmo faktorje:
V obeh primerih dobimo odgovor 15, kar pomeni, da lahko med izrazoma 3 × 5 in 5 × 3 postavimo znak enakosti, ker imata enak pomen:
In s pomočjo spremenljivk bo premični zakon množenja videti takole:
a × b = b × a
kje a in b- dejavniki
Kombinacijski zakon množenja
Ta zakon pravi, da če je izraz sestavljen iz več dejavnikov, potem izdelek ne bo odvisen od vrstnega reda dejanj.
Na primer, izraz 3 × 2 × 4 je sestavljen iz več faktorjev. Če ga želite izračunati, lahko najprej pomnožite 3 in 2, nato pa dobljeni produkt pomnožite s preostalo številko 4. Videti bo tako:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
To je bila prva rešitev. Druga možnost je, da lahko najprej pomnožite 2 in 4, nato pa dobljeni produkt pomnožite s preostalo številko 3. Videti bo takole:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
V obeh primerih dobimo odgovor 24. Zato lahko med izrazi in, ker imajo enak pomen, postavite znak enakosti:
(3 × 2) × 4 = 3 × (2 × 4)
in z uporabo spremenljivk zakon o kombinaciji množenje lahko zapišemo takole:
a × b × c = (a × b) × c = a × (b × c)
kje namesto a, b,c poljubne številke so lahko.
Zakon o distribucijskem množenju
Ta zakon smo preučili v lekciji. Ponovimo še enkrat.
Porazdelitveni zakon množenja vam omogoča, da količino pomnožite s številom. Da bi to naredili, se vsak člen v tej vsoti pomnoži s to številko in rezultati seštejejo.
Na primer, poiščimo vrednost izraza (2 + 3) × 5
Izraz v oklepaju je vsota. To vsoto je treba pomnožiti s številom 5. Za to je treba vsak člen te vsote, to je številki 2 in 3, pomnožiti s številom 5 in dobljeni rezultati sešteti:
![]()
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Torej je vrednost izraza (2 + 3) × 5 25.
Z uporabo spremenljivk je zakon porazdelitve množenja zapisan takole:
(a + b) × c = a × c + b × c
kje namesto a, b, c poljubne številke so lahko.
Zakon množenja z ničlo
Ta zakon pravi, da če je v katerem koli množenju vsaj ena nič, bo odgovor nič. Zakon izgleda takole:
Zmnožek je enak nič, če je vsaj eden od faktorjev enak nič.
Na primer, izraz 0 × 2 je nič
Postavlja se vprašanje "zakaj se to dogaja?" V tem primeru je dva množitelj in kaže, kolikokrat je treba množitelj povečati. To pomeni, kolikokrat povečati ničlo. Dobesedno se ta izraz glasi "dvojna ničla". Toda kako se lahko nič podvoji, če je nič?
Z drugimi besedami, če se "nič" podvoji ali celo milijonkrat večje, boste še vedno dobili "nič".
In če zamenjate faktorje v izrazu 0 × 2, boste spet dobili nič. To vemo iz prejšnjega zakona o prenosu:
Primeri uporabe zakona množenja z ničlo:
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
V zadnjih dveh primerih je več dejavnikov. Ko v njih vidimo nič, v odgovor takoj postavimo nič, pri čemer uporabimo zakon množenja z ničlo.
Obravnavali smo osnovne zakone množenja. Nato razmislite o množenju celih števil.
Celoštevilno množenje
Primer 1. Poiščite vrednost izraza −5 × 2
To je množenje števil z različnimi znaki. −5 je negativno, 2 pa pozitivno. V takih primerih je treba uporabiti naslednje pravilo:
Če želite pomnožiti števila z različnimi predznaki, morate pomnožiti njihove module in pred odgovor postaviti znak minus.
−5 × 2 = - (| −5 | × | 2 |) = - (5 × 2) = - (10) = −10
Običajno napisano krajše: −5 × 2 = −10
Postavlja se vprašanje "zakaj se to dogaja?" Dejstvo je, da je vsako množenje mogoče predstaviti kot vsoto števil. Na primer, upoštevajte izraz 2 × 3. Enak je 6.
Faktor v tem izrazu je število 3. Ta faktor kaže, kolikokrat morate povečati dva. Toda izraz 2 × 3 lahko predstavimo tudi kot vsoto treh dvojic:
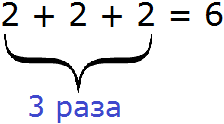
Enako se zgodi z izrazom −5 × 2. Ta izraz lahko predstavimo kot vsoto
![]()
In izraz (−5) + (−5) je enak −10 in ga poznamo iz. To je seštevanje negativnih številk. Spomnimo se, da je rezultat seštevanja negativnih števil negativno število.
Primer 2. Poiščite vrednost izraza 12 × (−5)
To je množenje števil z različnimi predznaki. 12 je pozitivno število, (−5) je negativno. Ponovno uporabimo prejšnje pravilo. Pomnožimo module številk in pred prejetim odgovorom postavimo znak minus:
12 × (−5) = - (| 12 | × | −5 |) = - (12 × 5) = - (60) = −60
Običajno napisano krajše: 12 × (−5) = −60
Primer 3. Poiščite vrednost izraza 10 × (−4) × 2
Ta izraz je sestavljen iz več dejavnikov. Najprej pomnožite 10 in (−4), nato pa dobljeno število pomnožite z 2. Na poti uporabite prej preučena pravila:
Prvo dejanje:
10 × (−4) = - (| 10 | × | −4 |) = - (10 × 4) = (−40) = −40
Drugo dejanje:
−40 × 2 = - (| −40 | × | 2 |) = - (40 × 2) = - (80) = −80
Torej je vrednost izraza 10 × (−4) × 2 −80
Običajno napisano krajše: 10 × (−4) × 2 = −40 × 2 = −80
Primer 4. Poiščite vrednost izraza (−4) × (−2)
To je množenje negativnih števil. V takih primerih je treba uporabiti naslednje pravilo:
Če želite pomnožiti negativna števila, morate pomnožiti njihove module in pred prejetim odgovorom postaviti znak plus
(−4) × (−2) = | −4 | × | −2 | = 4 × 2 = 8
Poleg tega po tradiciji ne pišemo, zato samo zapišemo odgovor 8.
Običajno se zapiše krajše (−4) × (−2) = 8
Postavlja se vprašanje, zakaj pri množenju negativnih števil nenadoma dobiš pozitivno število. Poskusimo dokazati, da je (−4) × (−2) 8 in nič drugega.
Najprej napišemo naslednji izraz:
Postavimo ga v oklepaje:
(4 × (−2))
Temu izrazu dodajmo naš izraz (−4) × (−2). V oklepaje ga zapremo tudi:
(4 × (−2)) + ((−4) × (−2))
Izenačimo vse to z ničlo:
(4 × (−2)) + ((−4) × (−2)) = 0
Zdaj se zabava začne. Bistvo je, da moramo oceniti levo stran tega izraza in kot rezultat dobimo 0.
Torej je prvi produkt (4 × (−2)) −8. V naš izraz zapišemo število −8 namesto produkta (4 × (−2))
−8 + ((−4) × (−2)) = 0
Zdaj namesto drugega dela začasno postavite tritočko
−8 + […] = 0
Zdaj pa natančno poglejte izraz −8 + […] = 0. Katero število mora biti na mestu elipse, da se ohrani enakost? Odgovor se nakazuje sam od sebe. Namesto elipse naj bo pozitivna številka 8 in nobena druga. Samo na ta način bo spoštovana enakost. Konec koncev je −8 + 8 enako 0.
Vrnemo se k izrazu −8 + ((−4) × (−2)) = 0 in namesto produkta ((−4) × (−2)) zapišemo število 8
Primer 5. Poiščite vrednost izraza −2 × (6 + 4)
Uporabljamo distribucijski zakon množenja, to pomeni, da število −2 pomnožimo z vsakim členom vsote (6 + 4)
−2 × (6 + 4) = (−2 × 6) + (−2 × 4)
Zdaj pa ocenimo izraze v oklepajih. Nato rezultate seštejemo. Na poti bomo uporabljali prej naučena pravila. Vnos z moduli lahko preskočite, da ne zamašite izraza
Prvo dejanje:
−2 × 6 = - (2 × 6) = - (12) = −12
Drugo dejanje:
−2 × 4 = - (2 × 4) = - (8) = −8
Tretje dejanje:
−12 + (−8) = −20
Torej je vrednost izraza −2 × (6 + 4) −20
Običajno napisano krajše: −2 × (6 + 4) = (−12) + (−8) = −20
Primer 6. Poiščite vrednost izraza (−2) × (−3) × (−4)
Izraz je sestavljen iz več dejavnikov. Najprej pomnožite številki −2 in −3 ter dobljeni produkt pomnožite s preostalim številom −4. Preskočimo zapis z moduli, da ne zamašimo izraza
Prvo dejanje:
(−2) × (−3) = 6
Drugo dejanje:
6 × (−4) = - (6 × 4) = −24
Torej je vrednost izraza (−2) × (−3) × (−4) −24
Običajno napisano krajše: (−2) × (−3) × (−4) = 6 × (−4) = −24
Zakoni o delitvah
Pred deljenjem celih števil se je treba naučiti dva zakona deljenja.
Najprej se spomnimo, iz česa je sestavljena delitev. Razdelek je sestavljen iz treh parametrov: dividende, delilnik in zasebni... Upoštevajte na primer najpreprostejši izraz:
Tukaj je 8 dividenda, 2 je delilec, 4 je količnik.

dividenda pokaže, kaj točno delimo. V našem primeru delimo število 8.
delilnik prikazuje, na koliko delov je treba razdeliti dividendo. V našem primeru je delilec številka 2. Ta delilec kaže, na koliko delov je treba deliti dividendo 8. To pomeni, da bo med operacijo delitve število 8 razdeljeno na dva dela.
Zasebno Je dejanski rezultat operacije delitve. V našem primeru je količnik 4. Ta količnik je rezultat deljenja 8 z 2.
Ne morete deliti z nič
Vsako število je prepovedano deliti z nič. Vprašanje "zakaj?"
Bistvo je, da je deljenje obratno od množenja. Na primer, če je 2 × 6 = 12, potem je 12: 6 = 2
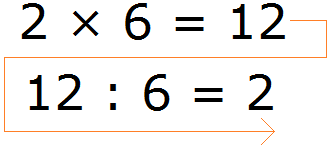
Vidimo, da je drugi izraz zapisan v obratnem vrstnem redu.
Zdaj naredimo enako za izraz 5 × 0. Iz zakonov množenja vemo, da je produkt enak nič, če je vsaj eden od faktorjev enak nič. Torej je izraz 5 × 0 enak nič
Če ta izraz zapišemo v obratnem vrstnem redu, dobimo:
Odgovor takoj pade v oči, kar je rezultat delitve nič z ničlo. To je nemogoče in neumno.
V obratnem vrstnem redu lahko napišete še en podoben izraz, na primer 2 × 0 = 0
V prvem primeru z deljenjem nič z nič dobimo 5, v drugem primeru pa 2. Se pravi, vsakič, ko delimo nič z nič, lahko dobimo različne vrednosti, kar je v matematiki nesprejemljivo.
To je bila prva razlaga, zakaj ne morete deliti z nič.
Druga razlaga je, da deljenje dividende z delilnikom pomeni najti število, ki, ko se pomnoži z delilnikom, daje dividendo.
Na primer, izraz 8: 2 pomeni najti število, ki bo, če ga pomnožimo z 2, dalo 8
Tukaj naj bo namesto elipse številka, ki po množenju z 2 daje odgovor 8. Za iskanje tega števila je dovolj, da ta izraz zapišemo v obratnem vrstnem redu:
Zdaj si predstavljajte, da morate najti vrednost izraza 5: 0. V tem primeru je 5 dividenda, 0 pa je delilec. Deljenje 5 z 0 pomeni iskanje števila, ki, če ga pomnožimo z 0, da 5
Tukaj bi morala biti namesto elipse število, ki pri množenju z 0 daje odgovor 5. Ni pa števila, ki bi pri množenju z ničlo dalo 5.
Izraz […] × 0 = 5 je v nasprotju z zakonom množenja z nič, ki pravi, da je produkt enak nič, če je vsaj eden od faktorjev enak nič.
To pomeni, da nima smisla pisati izraza [...] × 0 = 5 v obratnem vrstnem redu, deliti 5 z 0. Zato pravijo, da ne moreš deliti z nič.
Z uporabo spremenljivk je ta zakon zapisan takole:
Pri b ≠ 0
Številka a lahko delimo s številom b, pod pogojem, da b ni nič.
Zasebna last
Ta zakon pravi, da če se dividenda in delilec pomnožita ali delita z istim številom, se količnik ne bo spremenil.
Upoštevajte na primer izraz 12: 4. Vrednost tega izraza je 3

Poskusimo pomnožiti deljenec in delilec z istim številom, na primer s številom 4. Če verjamemo v lastnost količnika, bi morali v odgovoru spet dobiti številko 3

(12 × 4): (4 × 4)
(12 × 4): (4 × 4) = 48: 16 = 3
Odgovor je bil 3.
Zdaj pa poskusimo ne množiti, ampak deliti dividendo in delilec s številom 4
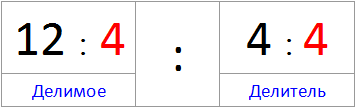
(12: 4 ) : (4: 4 )
(12: 4 ) : (4: 4 ) = 3: 1 = 3
Odgovor je bil 3.
Vidimo, da če se dividenda in delilec pomnožita ali delita z istim številom, se količnik ne spremeni.
Deljenje celih števil
Primer 1. Poiščite vrednost izraza 12: (−2)
To je delitev števil z različnimi znaki. 12 je pozitivno število, (−2) je negativno. V takih primerih potrebujete
12: (−2) = −(|12| : |−2|) = −(12: 2) = −(6) = −6
Običajno se zapiše krajše od 12: (−2) = −6
Primer 2. Poiščite vrednost izraza −24: 6
To je delitev števil z različnimi znaki. −24 je negativno, 6 je pozitivno. V takih primerih spet potrebujete delimo modul dividende z modulom delitelja in pred prejetim odgovorom postavimo znak minus.
−24: 6 = −(|−24| : |6|) = −(24: 6) = −(4) = −4
Običajno je napisano krajše od -24: 6 = -4
Primer 3. Poiščite vrednost izraza (−45): (−5)
To je delitev negativnih števil. V takih primerih potrebujete delimo modul dividende z modulom delitelja in pred prejetim odgovorom postavimo znak plus.
(−45) : (−5) = |−45| : |−5| = 45: 5 = 9
Običajno napisano krajše (-45): (-5) = 9
Primer 4. Poiščite vrednost izraza (−36): (−4): (−3)
V skladu s tem, če izraz vsebuje samo množenje ali deljenje, je treba vsa dejanja izvesti od leve proti desni v vrstnem redu, ki jim sledi.
(−36) delite s (−4) in dobljeno število delite s (−3)
Prvo dejanje:
(−36) : (−4) = |−36| : |−4| = 36: 4 = 9
Drugo dejanje:
9: (−3) = −(|−9| : |−3|) = −(9: 3) = −(3) = −3
Običajno napisano krajše (-36): (-4): (-3) = 9: (-3) = -3
Vam je bila lekcija všeč?
Pridružite se našemu nova skupina Vkontakte in začnite prejemati obvestila o novih lekcijah
Cele številke - to so naravna števila, pa tudi njihova nasprotna števila in nič.
Cela števila- razširitev množice naravnih števil N ki ga dobimo z dodajanjem k N 0 in negativna števila, kot je - n... Nabor celih števil označuje Z.
Vsota, razlika in zmnožek celih števil daje spet cela števila, t.j. cela števila tvorijo obroč glede na operacije seštevanja in množenja.
Cela števila na številski osi:
Koliko celih števil? Koliko celih števil? Ne obstaja največje ali najmanjše celo število. Serija je neskončna. Največje in najmanjše celo število ne obstajata.
Imenujejo se tudi naravna števila pozitivno cela števila, tj. besedna zveza "naravno število" in "pozitivno celo število" sta eno in isto.
Niti ulomki niti decimalke niso cela števila. Vendar obstajajo ulomki s celimi števili.
Primeri celih števil: -8, 111, 0, 1285642, -20051 itd.
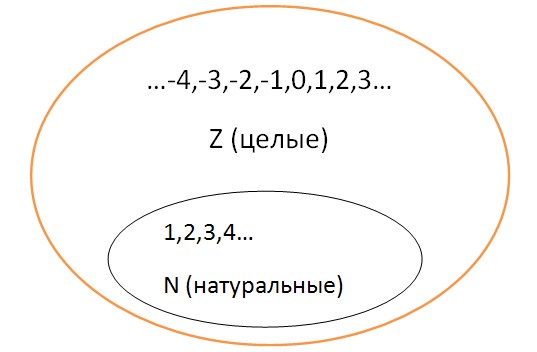
govorjenje preprost jezik, cela števila so (∞... -4,-3,-2,-1,0,1,2,3,4...+ ∞) - zaporedje celih števil. To pomeni tiste, pri katerih je ulomni del (()) enak nič. Nimajo vložkov.
Naravna števila so cela števila, pozitivne številke... cele številke, primeri: (1,2,3,4...+ ∞).
Operacije nad celimi števili.
1. Vsota celih števil.
Za seštevanje dveh celih števil z istimi predznakoma je potrebno sešteti module teh številk in pred vsoto postaviti končni predznak.
Primer:
(+2) + (+5) = +7.
2. Odštevanje celih števil.
Za seštevanje dveh celih števil z različnimi znaki je potrebno od modula števila, ki je več, odšteti modul števila, ki je manjši, in pred odgovor postaviti znak več modulo.
Primer:
(-2) + (+5) = +3.
3. Množenje celih števil.
Za množenje dveh celih števil je potrebno pomnožiti module teh številk in pred zmnožek postaviti znak plus (+), če sta bila prvotna števila enakega predznaka, in minus (-), če sta različni.
Primer:
(+2) ∙ (-3) = -6.
Ko se pomnoži več številk, bo predznak produkta pozitiven, če je število nepozitivnih faktorjev sodo, in negativen, če je liho.
Primer:
(-2) ∙ (+3) ∙ (-5) ∙ (-3) ∙ (+4) = -360 (3 nepozitivni dejavniki).
4. Deljenje celih števil.
Za deljenje celih števil je potrebno modul enega deliti z modulom drugega in pred rezultat postaviti znak "+", če sta predznaka števil enaka, in minus, če sta različna.
Primer:
(-12) : (+6) = -2.
Lastnosti celih števil.
Z ni zaprt z deljenjem 2 celih števil ( npr. 1/2). Spodnja tabela prikazuje nekaj osnovnih lastnosti seštevanja in množenja za vsa cela števila. a, b in c.
|
Lastnina |
dodatek |
množenje |
|
izolacija |
a + b- cela |
a × b- cela |
|
asociativnost |
a + (b + c) = (a + b) + c |
a × ( b × c) = (a × b) × c |
|
zmenljivost |
a + b = b + a |
a × b = b × a |
|
Obstoj nevtralen element |
a + 0 = a |
a × 1 = a |
|
Obstoj nasprotni element |
a + (−a) = 0 |
a ≠ ± 1 ⇒ 1 / a ni cela |
|
distributivnost množenje glede na dodatki |
a × ( b + c) = (a × b) + (a × c) |
|
Iz tabele lahko sklepamo, da Z je komutativni obroč z enoto glede na seštevanje in množenje.
Standardna delitev na množici celih števil ne obstaja, obstaja pa ti delitev preostanka: za vse vrste celote a in b, b ≠ 0, obstaja en niz celih števil q in r, kaj a = bq + r in 0≤r<|b| , kje | b |- absolutna vrednost (modul) števila b... tukaj a- dividenda, b- delilnik, q- zasebno, r- preostanek.



