ผลคูณของกฎจำนวนเต็ม การคูณและหารจำนวนเต็ม กฎการคูณของการคูณ

มีการใช้กฎหลายข้อในการคูณและหารจำนวนเต็ม ในบทนี้เราจะดูแต่ละรายการ

เมื่อคูณและหารจำนวนเต็ม ให้ใส่ใจกับเครื่องหมายของตัวเลข มันจะขึ้นอยู่กับพวกเขาว่าจะใช้กฎใด นอกจากนี้จำเป็นต้องศึกษากฎการคูณและการหารหลายข้อด้วย การศึกษากฎเหล่านี้ช่วยให้คุณหลีกเลี่ยงข้อผิดพลาดที่น่ารำคาญในอนาคต

เนื้อหาบทเรียน

กฎการคูณ

เราดูกฎของคณิตศาสตร์บางข้อในบทเรียน แต่เราไม่ได้พิจารณากฎหมายทั้งหมด คณิตศาสตร์มีกฎอยู่หลายข้อ และควรศึกษากฎเหล่านี้ตามลำดับตามความจำเป็นจะดีกว่า

ก่อนอื่น จำไว้ว่าการคูณประกอบด้วยอะไรบ้าง การคูณประกอบด้วยสามพารามิเตอร์: ทวีคูณ, ตัวคูณและ ทำงาน

โดยที่ 3 คือตัวคูณ 2 คือตัวคูณ 6 คือผลคูณ

ทวีคูณแสดงให้เห็นว่าเรากำลังเพิ่มขึ้นอย่างแน่นอน ในตัวอย่างของเรา เราเพิ่มเลข 3

ปัจจัยแสดงจำนวนครั้งที่คุณต้องเพิ่มตัวคูณ ในตัวอย่างของเรา ตัวคูณคือเลข 2 ตัวคูณนี้แสดงว่าต้องเพิ่มตัวคูณ 3 กี่ครั้ง นั่นคือในระหว่างการคูณเลข 3 จะเพิ่มเป็นสองเท่า

งาน -นี่คือผลลัพธ์ที่แท้จริงของการดำเนินการคูณ ในตัวอย่างของเรา ผลคูณคือเลข 6 ผลคูณนี้คือผลลัพธ์ของการคูณ 3 ด้วย 2

นิพจน์ 3 × 2 สามารถเข้าใจได้ว่าเป็นผลรวมของแฝดสองตัว ตัวคูณ 2 นิ้ว ในกรณีนี้จะแสดงจำนวนครั้งที่คุณต้องเพิ่มแฝดสาม:

กฎการสับเปลี่ยนของการคูณ

เราได้ดูกฎการสลับของการคูณไปแล้วในบทเรียน มาทำซ้ำอีกครั้ง

ตัวคูณและตัวคูณถูกเรียกด้วยคำทั่วไปเพียงคำเดียว - ปัจจัย- กฎการคูณสับเปลี่ยนมีดังนี้:

การจัดเรียงสถานที่ของปัจจัยใหม่ไม่ทำให้ผลิตภัณฑ์เปลี่ยนแปลง

มาตรวจสอบว่าสิ่งนี้เป็นจริงหรือไม่ ตัวอย่างเช่น ลองคูณ 3 ด้วย 5 โดยที่ 3 และ 5 คือตัวประกอบ

ทีนี้มาสลับปัจจัยกัน:

ในทั้งสองกรณี เราได้คำตอบ 15 ซึ่งหมายความว่าเราสามารถใส่เครื่องหมายเท่ากับระหว่างนิพจน์ 3 × 5 และ 5 × 3 ได้ เนื่องจากเครื่องหมายทั้งสองมีความหมายเหมือนกัน:

และด้วยความช่วยเหลือของตัวแปร กฎการคูณการสับเปลี่ยนจะมีลักษณะดังนี้:

ก × ข = ข × ก

ที่ไหน กและ ข- ปัจจัย

กฎการคูณของการคูณ

กฎข้อนี้กล่าวว่าหากนิพจน์ประกอบด้วยหลายปัจจัย ผลิตภัณฑ์นั้นจะไม่ขึ้นอยู่กับลำดับของการกระทำ

ตัวอย่างเช่น นิพจน์ 3 × 2 × 4 ประกอบด้วยหลายปัจจัย ในการคำนวณ คุณสามารถคูณ 3 และ 2 ก่อน จากนั้นคูณผลลัพธ์ที่ได้ด้วยจำนวน 4 ที่เหลือ ซึ่งจะมีลักษณะดังนี้:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

นี่เป็นวิธีแก้ปัญหาแรก ตัวเลือกที่สองคือคุณสามารถคูณ 2 และ 4 ได้ก่อน จากนั้นจึงคูณผลลัพธ์ที่ได้ด้วยจำนวน 3 ที่เหลือ ซึ่งจะมีลักษณะดังนี้:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

ในทั้งสองกรณี เราได้คำตอบว่า 24 ดังนั้น เราสามารถใส่เครื่องหมายเท่ากับระหว่างสำนวนเหล่านี้ได้ และเนื่องจากสำนวนเหล่านี้มีความหมายเหมือนกัน:

(3 × 2) × 4 = 3 × (2 × 4)

และด้วยความช่วยเหลือของตัวแปร กฎการเชื่อมโยงของการคูณสามารถเขียนได้ดังนี้:

ก × ข × ค = (ก × ข) × ค = ก × (ข × ค)

ที่ไหนแทน ก, ข,คสามารถเป็นตัวเลขใดก็ได้

กฎการกระจายของการคูณ

เราศึกษากฎหมายนี้ในบทเรียน มาทำซ้ำอีกครั้ง

กฎการกระจายของการคูณทำให้คุณสามารถคูณผลรวมด้วยตัวเลขได้ ในการทำเช่นนี้ แต่ละเทอมของผลรวมนี้จะถูกคูณด้วยตัวเลขนี้ และผลลัพธ์ที่ได้จะถูกบวกเข้าไปด้วย

ตัวอย่างเช่น ลองหาค่าของนิพจน์ (2 + 3) × 5

นิพจน์ในวงเล็บคือผลรวม ผลรวมนี้จะต้องคูณด้วยเลข 5 ในการทำเช่นนี้แต่ละเทอมของผลรวมนี้ซึ่งก็คือตัวเลข 2 และ 3 จะต้องคูณด้วยเลข 5 และผลลัพธ์ที่ได้จะบวก:

(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

ซึ่งหมายความว่าค่าของนิพจน์ (2 + 3) × 5 คือ 25

การใช้ตัวแปร กฎการกระจายของการคูณเขียนได้ดังนี้:

(a + b) × c = a × c + b × c

ที่ไหนแทน ก ข คสามารถเป็นตัวเลขใดก็ได้

กฎการคูณด้วยศูนย์

กฎข้อนี้บอกว่าถ้ามีศูนย์อย่างน้อยหนึ่งตัวในการคูณ คำตอบจะเป็นศูนย์ กฎหมายมีลักษณะดังนี้:

ผลคูณจะเท่ากับศูนย์ถ้ามีตัวประกอบอย่างน้อยหนึ่งตัวเท่ากับศูนย์

ตัวอย่างเช่น นิพจน์ 0 × 2 เท่ากับศูนย์

คำถามเกิดขึ้น: “ทำไมสิ่งนี้ถึงเกิดขึ้น?” ในกรณีนี้ สองคือตัวคูณและแสดงว่าต้องเพิ่มตัวคูณกี่ครั้ง นั่นคือกี่ครั้งที่จะเพิ่มศูนย์ ตามตัวอักษร สำนวนนี้อ่านว่า "ศูนย์สองเท่า" แต่คุณจะเพิ่มศูนย์เป็นสองเท่าได้อย่างไรถ้าเป็นศูนย์?

กล่าวอีกนัยหนึ่ง ถ้า “ไม่มีอะไร” เพิ่มเป็นสองเท่า หรือแม้แต่ล้านครั้ง มันก็จะยังคงเป็น “ไม่มีอะไร”

และถ้าคุณสลับตัวประกอบในนิพจน์ 0 × 2 คุณจะได้ศูนย์อีกครั้ง เรารู้สิ่งนี้จากกฎการเคลื่อนที่ครั้งก่อน:

ตัวอย่างการใช้กฎการคูณด้วยศูนย์:

5 × 5 × 5 × 0 = 0

2 × 5 × 0 × 9 × 1 = 0

ในสองตัวอย่างสุดท้ายมีหลายปัจจัย เมื่อเห็นศูนย์แล้ว เราก็ใส่ศูนย์ลงในคำตอบทันที โดยใช้กฎการคูณด้วยศูนย์

เราดูกฎพื้นฐานของการคูณ ต่อไปเรามาดูการคูณจำนวนเต็มกัน

การคูณจำนวนเต็ม

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ −5 × 2

นี่คือการคูณตัวเลขด้วย สัญญาณที่แตกต่างกัน- −5 เป็นจำนวนลบ และ 2 เป็นจำนวนบวก ในกรณีดังกล่าว ควรใช้กฎต่อไปนี้:

หากต้องการคูณตัวเลขด้วยเครื่องหมายต่างกัน คุณต้องคูณโมดูลของตัวเลขเหล่านั้นและใส่เครื่องหมายลบไว้หน้าคำตอบที่ได้

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

โดยปกติจะเขียนสั้นกว่า: −5 × 2 = −10

คำถามเกิดขึ้น: “ทำไมสิ่งนี้ถึงเกิดขึ้น?” ความจริงก็คือการคูณใดๆ สามารถแสดงเป็นผลรวมของตัวเลขได้ ตัวอย่างเช่น พิจารณานิพจน์ 2 × 3 ซึ่งเท่ากับ 6

ตัวคูณเข้า ได้รับการแสดงออกคือเลข 3 ตัวคูณนี้จะแสดงจำนวนครั้งที่คุณต้องเพิ่มทั้งสอง แต่นิพจน์ 2 × 3 สามารถแสดงเป็นผลรวมของ 3 สองได้:

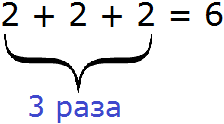
สิ่งเดียวกันนี้เกิดขึ้นกับนิพจน์ −5 × 2 นิพจน์นี้สามารถแสดงเป็นผลรวมได้

และนิพจน์ (−5) + (−5) เท่ากับ −10 และเรารู้สิ่งนี้จาก นี่คือการบวกจำนวนลบ จำไว้ว่าผลลัพธ์ของการบวกจำนวนลบก็คือจำนวนลบ

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 12 × (−5)

นี่คือการคูณตัวเลขที่มีเครื่องหมายต่างกัน 12 เป็นจำนวนบวก (−5) เป็นจำนวนลบ เราใช้กฎก่อนหน้านี้อีกครั้ง เราคูณโมดูลของตัวเลขและใส่เครื่องหมายลบหน้าคำตอบผลลัพธ์:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

มักจะเขียนสั้นกว่า: 12 × (−5) = −60

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 10 × (−4) × 2

นิพจน์นี้ประกอบด้วยหลายปัจจัย ขั้นแรก คูณ 10 และ (−4) จากนั้นคูณจำนวนผลลัพธ์ด้วย 2 ให้ใช้กฎที่เรียนรู้มาก่อนหน้านี้ไปพร้อมกัน:

การกระทำครั้งแรก:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

การกระทำที่สอง:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

ดังนั้นค่าของนิพจน์ 10 × (−4) × 2 คือ −80

มักจะเขียนสั้นกว่า: 10 × (−4) × 2 = −40 × 2 = −80

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ (−4) × (−2)

นี่คือการคูณจำนวนลบ ในกรณีเช่นนี้ ต้องใช้กฎต่อไปนี้:

หากต้องการคูณจำนวนลบ คุณต้องคูณโมดูลของจำนวนเหล่านั้นและใส่เครื่องหมายบวกหน้าคำตอบที่ได้

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

นอกจากนี้ ตามธรรมเนียมแล้ว เราไม่ได้เขียน ดังนั้น เราจึงเขียนคำตอบไว้เพียง 8 เท่านั้น

มักจะเขียนสั้นกว่า (−4) × (−2) = 8

คำถามเกิดขึ้น: เหตุใดการคูณจำนวนลบจึงทำให้เกิดจำนวนบวก? ลองพิสูจน์ว่า (−4) × (−2) เท่ากับ 8 และไม่มีอะไรอื่นอีก

ขั้นแรกเราเขียนนิพจน์ต่อไปนี้:

มาใส่ไว้ในวงเล็บ:

(4 × (−2))

ลองเพิ่มนิพจน์ของเรา (−4) × (−2) เข้าไปในนิพจน์นี้ มาใส่ไว้ในวงเล็บด้วย:

(4 × (−2)) + ((−4) × (−2))

ลองถือเอาทั้งหมดนี้ให้เป็นศูนย์:

(4 × (−2)) + ((−4) × (−2)) = 0

ตอนนี้ความสนุกเริ่มต้นขึ้นแล้ว ประเด็นคือเราต้องประเมินทางด้านซ้ายของนิพจน์นี้แล้วได้ผลลัพธ์เป็น 0

ดังนั้นผลคูณแรก (4 × (−2)) คือ −8 ลองเขียนตัวเลข −8 ในนิพจน์ของเราแทนผลคูณ (4 × (−2))

−8 + ((−4) × (−2)) = 0

ตอนนี้แทนที่จะเป็นงานที่สอง เราจะใส่จุดไข่ปลาชั่วคราว

−8 + […] = 0

ตอนนี้เรามาดูนิพจน์ −8 + […] = 0 อย่างละเอียด ตัวเลขใดที่ควรปรากฏแทนจุดไข่ปลาเพื่อรักษาความเท่าเทียมกัน คำตอบนั้นบ่งบอกตัวมันเอง แทนที่จะเป็นจุดไข่ปลา ควรเป็นเลขบวก 8 และไม่มีอย่างอื่นอีก นี่เป็นวิธีเดียวที่จะรักษาความเท่าเทียมกันได้ ท้ายที่สุด −8 + 8 เท่ากับ 0

เรากลับไปที่นิพจน์ −8 + ((−4) × (−2)) = 0 และแทนที่จะเป็นผลคูณ ((−4) × (−2)) เราเขียนตัวเลข 8

ตัวอย่างที่ 5ค้นหาค่าของนิพจน์ −2 × (6 + 4)

ลองใช้กฎการกระจายของการคูณ กล่าวคือ คูณตัวเลข −2 ด้วยแต่ละเทอมของผลรวม (6 + 4)

−2 × (6 + 4) = (−2 × 6) + (−2 × 4)

ทีนี้ลองประเมินนิพจน์ในวงเล็บกัน จากนั้นเราจะรวมผลลัพธ์ที่ได้รับ ในระหว่างนี้ เราใช้กฎที่เรียนรู้มาก่อนหน้านี้ รายการที่มีโมดูลสามารถข้ามได้เพื่อไม่ให้เกะกะนิพจน์

การกระทำครั้งแรก:

−2 × 6 = −(2 × 6) = −(12) = −12

การกระทำที่สอง:

−2 × 4 = −(2 × 4) = −(8) = −8

การกระทำที่สาม:

−12 + (−8) = −20

ดังนั้นค่าของนิพจน์ −2 × (6 + 4) คือ −20

โดยปกติจะเขียนสั้นกว่า: −2 × (6 + 4) = (−12) + (−8) = −20

ตัวอย่างที่ 6ค้นหาค่าของนิพจน์ (−2) × (−3) × (−4)

การแสดงออกประกอบด้วยหลายปัจจัย ขั้นแรก คูณตัวเลข −2 และ −3 แล้วคูณผลคูณผลลัพธ์ด้วยจำนวนที่เหลือ −4 ข้ามรายการด้วยโมดูลเพื่อไม่ให้นิพจน์เกะกะ

การกระทำครั้งแรก:

(−2) × (−3) = 6

การกระทำที่สอง:

6 × (−4) = −(6 × 4) = −24

ดังนั้นค่าของนิพจน์ (−2) × (−3) × (−4) จึงเท่ากับ −24

โดยปกติจะเขียนสั้นกว่า: (−2) × (−3) × (−4) = 6 × (−4) = −24

กฎแห่งการแบ่งแยก

ก่อนที่จะหารจำนวนเต็ม คุณต้องเรียนรู้กฎการหารสองข้อก่อน

ก่อนอื่น เรามาจำไว้ว่าแผนกประกอบด้วยอะไรบ้าง การหารประกอบด้วยสามพารามิเตอร์: หารได้, ตัวหารและ ส่วนตัว- ตัวอย่างเช่น พิจารณานิพจน์ที่ง่ายที่สุด:

โดยที่ 8 คือเงินปันผล 2 คือตัวหาร 4 คือผลหาร

เงินปันผลแสดงให้เห็นว่าเรากำลังแบ่งปันอะไรกันแน่ ในตัวอย่างของเรา เรากำลังหารเลข 8

ตัวแบ่งแสดงว่าเงินปันผลจะต้องแบ่งเป็นกี่ส่วน ในตัวอย่างของเรา ตัวหารคือเลข 2 ตัวหารนี้แสดงจำนวนเงินปันผล 8 ที่ต้องหาร นั่นคือในระหว่างการหารเลข 8 จะถูกแบ่งออกเป็นสองส่วน

ส่วนตัว- นี่คือผลลัพธ์ที่แท้จริงของการดำเนินการของแผนก ในตัวอย่างของเรา ผลหารคือ 4 ผลหารนี้คือผลลัพธ์ของการหาร 8 ด้วย 2

คุณไม่สามารถหารด้วยศูนย์ได้

จำนวนใดๆ ไม่สามารถหารด้วยศูนย์ได้ คำถามเกิดขึ้น: "ทำไม"

ความจริงก็คือว่าการหารนั้นเป็นการดำเนินการผกผันของการคูณ เช่น ถ้า 2 × 6 = 12 แล้ว 12: 6 = 2

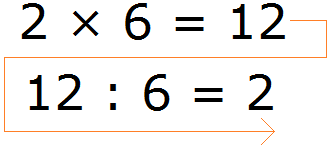
จะเห็นได้ว่านิพจน์ที่สองเขียนในลำดับย้อนกลับ

ตอนนี้เราจะทำแบบเดียวกันกับนิพจน์ 5 × 0 เรารู้จากกฎการคูณว่าผลคูณนั้นเท่ากับศูนย์ถ้าตัวประกอบอย่างน้อยหนึ่งตัวเท่ากับศูนย์ ซึ่งหมายความว่านิพจน์ 5 × 0 เท่ากับศูนย์

ถ้าเราเขียนนิพจน์นี้ในลำดับย้อนกลับ เราจะได้:

คำตอบที่สะดุดตาคุณทันทีคือ 5 ซึ่งได้มาจากการหารศูนย์ด้วยศูนย์ นี่เป็นไปไม่ได้และโง่เขลา

ในลำดับย้อนกลับ คุณสามารถเขียนนิพจน์อื่นที่คล้ายกันได้ เช่น 2 × 0 = 0

ในกรณีแรก การหาร 0 ด้วยศูนย์ เราได้ 5 และในกรณีที่สอง 2 นั่นคือ ทุกครั้งที่หาร 0 ด้วยศูนย์ เราจะได้ค่าที่แตกต่างกัน และนี่เป็นสิ่งที่ยอมรับไม่ได้ในวิชาคณิตศาสตร์

นี่เป็นคำอธิบายแรกว่าทำไมคุณไม่สามารถหารด้วยศูนย์ได้

คำอธิบายที่สองคือการหารเงินปันผลด้วยตัวหารหมายถึงการหาตัวเลขที่เมื่อคูณด้วยตัวหารแล้วจะได้เงินปันผล

ตัวอย่างเช่น นิพจน์ 8: 2 หมายถึงการค้นหาตัวเลขที่เมื่อคูณด้วย 2 จะได้ 8

ตรงนี้ แทนที่จะเป็นจุดไข่ปลา ควรมีตัวเลขที่เมื่อคูณด้วย 2 จะได้คำตอบ 8 หากต้องการค้นหาตัวเลขนี้ เพียงเขียนนิพจน์นี้ในลำดับย้อนกลับ:

ทีนี้ลองจินตนาการว่าคุณจำเป็นต้องค้นหาค่าของนิพจน์ 5: 0 ในกรณีนี้ 5 คือเงินปันผล และ 0 คือตัวหาร การหาร 5 ด้วย 0 หมายถึงการหาจำนวนที่เมื่อคูณด้วย 0 จะได้ 5

ในที่นี้ แทนที่จะเป็นจุดไข่ปลา ควรมีจำนวนตัวเลขที่เมื่อคูณด้วย 0 จะได้คำตอบ 5 แต่ไม่มีจำนวนใดที่เมื่อคูณด้วยศูนย์จะได้ 5

นิพจน์ […] × 0 = 5 ขัดแย้งกับกฎการคูณด้วยศูนย์ ซึ่งระบุว่าผลคูณเท่ากับศูนย์เมื่อมีตัวประกอบอย่างน้อยหนึ่งตัวเท่ากับศูนย์

ซึ่งหมายความว่าการเขียนนิพจน์ […] × 0 = 5 ในลำดับกลับกัน การหาร 5 ด้วย 0 นั้นไม่สมเหตุสมผล นั่นเป็นสาเหตุที่พวกเขาบอกว่าคุณไม่สามารถหารด้วยศูนย์ได้

การใช้ตัวแปรกฎหมายนี้เขียนดังนี้:

ที่ ข ≠ 0

ตัวเลข กสามารถหารด้วยตัวเลขได้ ขโดยมีเงื่อนไขว่า ขไม่เท่ากับศูนย์

ทรัพย์สินส่วนตัว

กฎข้อนี้บอกว่าถ้าเงินปันผลและตัวหารคูณหรือหารด้วยจำนวนเท่ากัน ผลหารจะไม่เปลี่ยนแปลง

ตัวอย่างเช่น พิจารณานิพจน์ 12: 4 ค่าของนิพจน์นี้คือ 3

ลองคูณเงินปันผลและตัวหารด้วยจำนวนเดียวกัน เช่น ด้วยเลข 4 ถ้าเราเชื่อคุณสมบัติของผลหาร เราก็ควรได้คำตอบเป็นเลข 3 อีกครั้ง

(12 × 4) : (4 × 4)

(12 × 4) : (4 × 4) = 48: 16 = 3

เราได้รับคำตอบข้อ 3

ทีนี้ลองอย่าคูณ แต่ให้หารเงินปันผลและตัวหารด้วยเลข 4

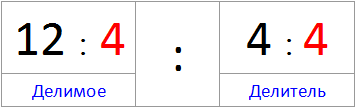
(12: 4 ) : (4: 4 )

(12: 4 ) : (4: 4 ) = 3: 1 = 3

เราได้รับคำตอบข้อ 3

เราจะเห็นว่าถ้าเงินปันผลและตัวหารคูณหรือหารด้วยจำนวนเท่ากัน ผลหารจะไม่เปลี่ยนแปลง

การหารจำนวนเต็ม

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 12: (−2)

นี่คือการหารตัวเลขที่มีเครื่องหมายต่างกัน 12 เป็นจำนวนบวก (−2) เป็นจำนวนลบ ในกรณีเช่นนี้ คุณจำเป็นต้อง

12: (−2) = −(|12| : |−2|) = −(12: 2) = −(6) = −6

โดยปกติจะเขียนสั้นกว่า 12: (−2) = −6

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ −24: 6

นี่คือการหารตัวเลขที่มีเครื่องหมายต่างกัน −24 เป็นจำนวนลบ 6 เป็นจำนวนบวก ในกรณีเช่นนี้ คุณต้องการอีกครั้ง แบ่งโมดูลของเงินปันผลด้วยโมดูลของตัวหาร และใส่เครื่องหมายลบหน้าคำตอบที่ได้

−24: 6 = −(|−24| : |6|) = −(24: 6) = −(4) = −4

มักจะเขียนสั้นกว่า −24: 6 = −4

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ (−45) : (−5)

นี่คือการหารจำนวนลบ ในกรณีเช่นนี้ คุณจำเป็นต้อง แบ่งโมดูลของเงินปันผลด้วยโมดูลของตัวหาร และใส่เครื่องหมายบวกหน้าคำตอบที่ได้

(−45) : (−5) = |−45| : |−5| = 45: 5 = 9

มักจะเขียนสั้นกว่า (−45) : (−5) = 9

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ (−36) : (−4) : (−3)

หากนิพจน์มีเพียงการคูณหรือการหาร การกระทำทั้งหมดจะต้องดำเนินการจากซ้ายไปขวาตามลำดับที่ปรากฏ

หาร (−36) ด้วย (−4) และหารจำนวนผลลัพธ์ด้วย (−3)

การกระทำครั้งแรก:

(−36) : (−4) = |−36| : |−4| = 36: 4 = 9

การกระทำที่สอง:

9: (−3) = −(|−9| : |−3|) = −(9: 3) = −(3) = −3

มักจะเขียนสั้นกว่า (−36) : (−4) : (−3) = 9: (−3) = −3

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกับเรา กลุ่มใหม่ VKontakte และเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่

ในบทความนี้เราจะมาดูวิธีการทำ การคูณจำนวนเต็ม- ก่อนอื่น เรามาแนะนำคำศัพท์และสัญลักษณ์ต่างๆ และหาความหมายของการคูณจำนวนเต็มสองตัวกันก่อน หลังจากนี้ เราจะได้กฎสำหรับการคูณจำนวนเต็มบวก จำนวนเต็มลบ และจำนวนเต็มที่มีเครื่องหมายต่างกัน ในเวลาเดียวกัน เราจะยกตัวอย่างพร้อมคำอธิบายโดยละเอียดเกี่ยวกับกระบวนการแก้ไขปัญหา นอกจากนี้ เราจะกล่าวถึงกรณีการคูณจำนวนเต็มเมื่อตัวประกอบตัวใดตัวหนึ่งมีค่าเท่ากับหนึ่งหรือศูนย์ ต่อไปเราจะเรียนรู้วิธีตรวจสอบผลลัพธ์การคูณ และสุดท้าย เรามาพูดถึงการคูณจำนวนเต็มสาม สี่ และจำนวนเต็มอื่นๆ กัน

การนำทางหน้า

ข้อกำหนดและสัญลักษณ์

เพื่ออธิบายการคูณจำนวนเต็ม เราจะใช้คำเดียวกับที่เราอธิบายการคูณจำนวนธรรมชาติ มาเตือนพวกเขากันเถอะ

จำนวนเต็มที่ถูกคูณเรียกว่า ตัวคูณ- เรียกว่าผลคูณ งาน- การคูณจะแสดงด้วยเครื่องหมายคูณในรูปแบบ "·" ในบางแหล่ง คุณจะพบสัญลักษณ์ “*” หรือ “×” สำหรับการคูณ

สะดวกในการเขียนจำนวนเต็มคูณ a, b และผลลัพธ์ของการคูณ c โดยใช้ความเท่าเทียมกันในรูปแบบ a·b=c ในสัญลักษณ์นี้ จำนวนเต็ม a คือตัวประกอบแรก จำนวนเต็ม b คือตัวประกอบที่สอง และจำนวนเต็ม c คือผลคูณ ของรูปแบบ a·b ก็จะถูกเรียกว่าผลิตภัณฑ์ เช่นเดียวกับค่าของนิพจน์นี้ c

เมื่อมองไปข้างหน้า เราสังเกตว่าผลคูณของจำนวนเต็มสองตัวแทนจำนวนเต็ม

ความหมายของการคูณจำนวนเต็ม

การคูณจำนวนเต็มบวก

จำนวนเต็มบวกก็คือตัวเลขธรรมชาติ ดังนั้น การคูณจำนวนเต็มบวกดำเนินการตามกฎทั้งหมดสำหรับการคูณจำนวนธรรมชาติ เห็นได้ชัดว่าการคูณจำนวนเต็มบวกสองตัวจะทำให้เกิดจำนวนเต็มบวก (จำนวนธรรมชาติ) ลองดูตัวอย่างสองสามตัวอย่าง

ตัวอย่าง.

ผลคูณของจำนวนเต็มบวก 127 และ 5 คืออะไร?

สารละลาย.

ลองนำเสนอตัวประกอบแรก 107 เป็นผลรวมของเทอมบิต ซึ่งก็คือ ในรูปแบบ 100+20+7 หลังจากนี้ เราใช้กฎในการคูณผลรวมของตัวเลขด้วยตัวเลขที่กำหนด: 127·5=(100+20+7)·5=100·5+20·5+7·5- สิ่งที่เหลืออยู่คือการคำนวณให้เสร็จสิ้น: 100·5+20·5+7·5= 500+100+35=600+35=635

ดังนั้น ผลคูณของจำนวนเต็มบวกที่กำหนด 127 และ 5 คือ 635

คำตอบ:

127·5=635.

หากต้องการคูณจำนวนเต็มบวกหลายหลัก จะสะดวกในการใช้วิธีการคูณคอลัมน์

ตัวอย่าง.

คูณจำนวนเต็มบวกสามหลัก 712 ด้วยจำนวนเต็มบวกสองหลัก 92

สารละลาย.

ลองคูณจำนวนเต็มบวกเหล่านี้ลงในคอลัมน์: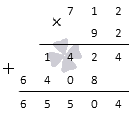

คำตอบ:

712·92=65,504.

กฎการคูณจำนวนเต็มด้วยเครื่องหมายต่างกัน ตัวอย่าง

ตัวอย่างต่อไปนี้จะช่วยเราในการกำหนดกฎสำหรับการคูณจำนวนเต็มด้วยเครื่องหมายต่างกัน

ลองคำนวณผลคูณของจำนวนเต็มลบ −5 และจำนวนเต็มกัน จำนวนบวก 3 ตามความหมายของการคูณ ดังนั้น (−5)·3=(−5)+(−5)+(−5)=−15- เพื่อให้สมบัติการสับเปลี่ยนของการคูณยังคงใช้ได้ ต้องได้ค่าความเท่ากัน (−5)·3=3·(−5) นั่นคือผลคูณ 3·(−5) ก็เท่ากับ −15 เช่นกัน มันง่ายที่จะเห็นว่า −15 เท่ากับสินค้าโมดูลัสของตัวประกอบดั้งเดิม ซึ่งตามมาว่าผลคูณของจำนวนเต็มดั้งเดิมที่มีเครื่องหมายต่างกันจะเท่ากับผลคูณของโมดูลัสของตัวประกอบดั้งเดิมที่นำมาด้วยเครื่องหมายลบ

ดังนั้นเราจึงได้ กฎการคูณจำนวนเต็มด้วยเครื่องหมายต่างกัน: หากต้องการคูณจำนวนเต็มสองตัวที่มีเครื่องหมายต่างกัน คุณต้องคูณโมดูลของตัวเลขเหล่านี้และใส่เครื่องหมายลบไว้หน้าตัวเลขผลลัพธ์

จากกฎที่ระบุ เราสามารถสรุปได้ว่าผลคูณของจำนวนเต็มที่มีเครื่องหมายต่างกันจะเป็นจำนวนเต็มลบเสมอ อันที่จริง จากการคูณโมดูลัสของปัจจัย เราจึงได้จำนวนเต็มบวก และถ้าเราใส่เครื่องหมายลบไว้หน้าตัวเลขนี้ มันจะกลายเป็นจำนวนเต็มลบ

ลองดูตัวอย่างการคำนวณผลคูณของจำนวนเต็มที่มีเครื่องหมายต่างกันโดยใช้กฎผลลัพธ์

ตัวอย่าง.

คูณจำนวนเต็มบวก 7 ด้วยจำนวนเต็มลบ −14

สารละลาย.

ลองใช้กฎในการคูณจำนวนเต็มด้วยเครื่องหมายต่างกัน โมดูลัสของตัวคูณคือ 7 และ 14 ตามลำดับ มาคำนวณผลคูณของโมดูลกัน: 7·14=98 สิ่งที่เหลืออยู่คือการใส่เครื่องหมายลบหน้าตัวเลขผลลัพธ์: −98 ดังนั้น 7·(−14)=−98

คำตอบ:

7·(−14)=−98 .

ตัวอย่าง.

คำนวณผลคูณ (−36)·29

สารละลาย.

เราจำเป็นต้องคำนวณผลคูณของจำนวนเต็มที่มีเครื่องหมายต่างกัน ในการทำเช่นนี้เราคำนวณผลคูณของค่าสัมบูรณ์ของปัจจัย: 36·29 = 1,044 (ควรคูณในคอลัมน์จะดีกว่า) ตอนนี้เราใส่เครื่องหมายลบหน้าหมายเลข 1044 เราได้ −1044

คำตอบ:

(−36)·29=−1,044 .

เพื่อสรุปย่อหน้านี้ เราจะพิสูจน์ความถูกต้องของความเท่าเทียมกัน a·(−b)=−(a·b) โดยที่ a และ −b เป็นจำนวนเต็มตามอำเภอใจ กรณีพิเศษของความเท่าเทียมกันนี้คือกฎที่ระบุไว้สำหรับการคูณจำนวนเต็มด้วยเครื่องหมายต่างกัน

กล่าวอีกนัยหนึ่ง เราต้องพิสูจน์ว่าค่าของนิพจน์ a·(−b) และ a·b เป็นจำนวนที่ตรงกันข้าม เพื่อพิสูจน์สิ่งนี้ ลองหาผลรวม a·(−b)+a·b แล้วตรวจสอบให้แน่ใจว่ามันเท่ากับศูนย์ เนื่องจากคุณสมบัติการกระจายของการคูณจำนวนเต็มสัมพันธ์กับการบวก ความเท่าเทียมกัน a·(−b)+a·b=a·((−b)+b) จึงเป็นจริง ผลรวม (−b)+b เท่ากับศูนย์เป็นผลรวมของจำนวนเต็มตรงข้าม จากนั้น a·((−b)+b)=a·0 ผลคูณสุดท้ายมีค่าเท่ากับศูนย์ด้วยคุณสมบัติของการคูณจำนวนเต็มด้วยศูนย์ ดังนั้น a·(−b)+a·b=0 ดังนั้น a·(−b) และ a·b จึงเป็นจำนวนที่ตรงกันข้าม ซึ่งแสดงถึงความถูกต้องของความเท่าเทียมกัน a·(−b)=−(a·b ) . ในทำนองเดียวกัน ก็สามารถแสดงได้ว่า (−a) b=−(ab)

กฎสำหรับการคูณจำนวนเต็มลบ ตัวอย่าง

ความเท่าเทียมกัน (−a)·(−b)=a·b ซึ่งเราจะพิสูจน์ในตอนนี้ จะช่วยให้เราได้กฎในการคูณจำนวนเต็มลบสองตัว

ในตอนท้ายของย่อหน้าก่อนหน้า เราแสดงให้เห็นว่า a·(−b)=−(a·b) และ (−a)·b=−(a·b) ดังนั้นเราจึงสามารถเขียนห่วงโซ่ความเท่าเทียมกันต่อไปนี้ (−a)·(−b)=−(a·(−b))=−(−(a·b))- และนิพจน์ผลลัพธ์ −(−(a·b)) ไม่มีอะไรมากไปกว่า a·b เนื่องจากนิยามของจำนวนตรงข้าม ดังนั้น (−a)·(−b)=a·b

ความเท่าเทียมกันที่พิสูจน์แล้ว (−a)·(−b)=a·b ช่วยให้เราสามารถกำหนดได้ กฎสำหรับการคูณจำนวนเต็มลบ: ผลคูณของจำนวนเต็มลบสองตัวเท่ากับผลคูณของโมดูลัสของตัวเลขเหล่านี้

จากกฎที่กล่าวมา ผลลัพธ์ของการคูณจำนวนเต็มลบสองตัวจะได้จำนวนเต็มบวก

ลองพิจารณาการใช้กฎนี้เมื่อทำการคูณจำนวนเต็มลบ

ตัวอย่าง.

คำนวณผลคูณของ (−34)·(−2) 1041 และ 538 มาทำการคูณคอลัมน์กัน: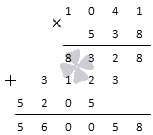

คำตอบ:

(−1,041)·(−538)=560,058 .

การคูณจำนวนเต็มด้วยหนึ่ง

การคูณจำนวนเต็ม a ด้วย 1 จะได้ผลลัพธ์เป็นจำนวน a เราได้กล่าวไปแล้วเมื่อเราพูดถึงความหมายของการคูณจำนวนเต็มสองตัว ดังนั้น a·1=a เนื่องจากสมบัติการสับเปลี่ยนของการคูณ ความเท่าเทียมกัน a·1=1·a จะต้องเป็นจริง ดังนั้น 1·a=a

เหตุผลข้างต้นนำเราไปสู่กฎสำหรับการคูณจำนวนเต็มสองตัว ซึ่งหนึ่งในนั้นมีค่าเท่ากับหนึ่ง ผลคูณของจำนวนเต็มสองตัวโดยที่ตัวประกอบตัวหนึ่งเป็นตัวหนึ่งจะเท่ากับตัวประกอบอีกตัวหนึ่ง.

ตัวอย่างเช่น 56·1=56, 1·0=0 และ 1·(−601)=−601 ลองยกตัวอย่างอีกสองสามตัวอย่าง ผลคูณของจำนวนเต็ม −53 และ 1 คือ −53 และผลิตภัณฑ์ของ 1 และจำนวนเต็มลบ −989,981 คือ −989,981

การคูณจำนวนเต็มด้วยศูนย์

เราตกลงกันว่าผลคูณของจำนวนเต็ม a และ 0 ใดๆ เท่ากับศูนย์ นั่นคือ a·0=0 สมบัติการสับเปลี่ยนของการคูณบังคับให้เรายอมรับความเท่าเทียมกัน 0·a=0 ดังนั้น, ผลคูณของจำนวนเต็มสองตัวโดยที่ตัวประกอบอย่างน้อยหนึ่งตัวเป็นศูนย์ก็เท่ากับศูนย์- โดยเฉพาะอย่างยิ่ง ผลลัพธ์ของการคูณศูนย์ด้วยศูนย์จะเป็นศูนย์: 0·0=0

ลองยกตัวอย่างบางส่วน ผลคูณของจำนวนเต็มบวก 803 และศูนย์เท่ากับศูนย์ ผลลัพธ์ของการคูณศูนย์ด้วยจำนวนเต็มลบ −51 จะเป็นศูนย์ ด้วย (−90 733)·0=0

โปรดทราบว่าผลคูณของจำนวนเต็มสองตัวจะเท่ากับศูนย์ก็ต่อเมื่อตัวประกอบอย่างน้อยหนึ่งตัวมีค่าเท่ากับศูนย์

การตรวจสอบผลลัพธ์ของการคูณจำนวนเต็ม

การตรวจสอบผลลัพธ์ของการคูณจำนวนเต็มสองตัวดำเนินการโดยใช้การแบ่ง จำเป็นต้องหารผลคูณผลลัพธ์ด้วยปัจจัยตัวใดตัวหนึ่ง หากผลลัพธ์เป็นตัวเลขเท่ากับตัวประกอบอื่น แสดงว่าการคูณทำได้ถูกต้อง หากผลลัพธ์เป็นตัวเลขที่แตกต่างจากคำอื่นแสดงว่ามีข้อผิดพลาดเกิดขึ้นที่ไหนสักแห่ง

ลองดูตัวอย่างที่มีการตรวจสอบผลลัพธ์ของการคูณจำนวนเต็ม

ตัวอย่าง.

จากการคูณจำนวนเต็มสองตัว −5 และ 21 จะได้ตัวเลข −115 ผลคูณคำนวณได้ถูกต้องหรือไม่ 5, −12, 1, −2 และ 15

สารละลาย.

เราสามารถแทนที่ตัวประกอบสองตัวที่อยู่ติดกันตามลำดับจากซ้ายไปขวาด้วยผลคูณของมัน: 5·(−12)·1·(−2)·15= (−60)·1·(−2)·15= (−60)· (−2 )·15= 120·15=1,800 ตัวเลือกสำหรับการคำนวณผลิตภัณฑ์นี้สอดคล้องกับวิธีการจัดวงเล็บดังต่อไปนี้: (((5·(−12))·1)·(−2))·15.

นอกจากนี้เรายังสามารถจัดเรียงปัจจัยบางอย่างใหม่และจัดวงเล็บให้แตกต่างออกไปได้ หากสิ่งนี้ช่วยให้เราคำนวณผลคูณของจำนวนเต็มทั้งห้าที่กำหนดได้อย่างมีประสิทธิภาพมากขึ้น ตัวอย่างเช่น คุณสามารถจัดเรียงปัจจัยใหม่ตามลำดับต่อไปนี้ 1·5·(−12)·(−2)·15 แล้วจัดเรียงวงเล็บดังนี้ ((1·5)·(−12))·((−2)·15)- ในกรณีนี้การคำนวณจะเป็นดังนี้: ((1·5)·(−12))·((−2)·15)=(5·(−12))·((−2)·15)= (−60)·(−30)=1 800 .

อย่างที่คุณเห็น ตัวเลือกที่แตกต่างกันการจัดวางวงเล็บเหลี่ยมและลำดับปัจจัยที่แตกต่างกันทำให้เราได้ผลลัพธ์เดียวกัน

คำตอบ:

5·(−12)·1·(−2)·15=1 800.

แยกกันเราทราบว่าหากในผลิตภัณฑ์มีสาม, สี่ ฯลฯ ของจำนวนเต็ม ตัวประกอบอย่างน้อยหนึ่งตัวมีค่าเท่ากับศูนย์ แล้วผลคูณจะเท่ากับศูนย์ ตัวอย่างเช่น ผลคูณของจำนวนเต็มสี่จำนวน 5, −90321, 0 และ 111 มีค่าเท่ากับศูนย์ ผลลัพธ์ของการคูณจำนวนเต็มสามจำนวน 0, 0 และ −1983 ก็เป็นศูนย์เช่นกัน สิ่งที่กลับกันก็เป็นจริงเช่นกัน หากผลคูณเท่ากับศูนย์ แสดงว่าปัจจัยอย่างน้อยหนึ่งตัวมีค่าเท่ากับศูนย์