Writing numbers in the decimal number system.
Comparison of numbers.
Addition.
Subtraction.
Multiplication.
1. Of all the positional number systems, the decimal system is now widely used. Therefore, we will dwell on writing and reading numbers in this system in more detail.
Definition 2. Decimal notation natural number X is called its representation in the form
where 0 ≤ A i ≤ 9 (i = 0, 1, ..., P), A P ≠ 0.
Numbers 1, 10, 10 2 , 10 3 , ..., 10 P are called here bit units, respectively, the first, second, third, etc. discharges.
The first three digits in the notation of a number are combined into one group and are called the first class, or unit class. The first class includes units, tens and hundreds.
The next three ranks - the fourth, fifth and sixth - form the second class, or thousands class. It includes units of thousands, tens of thousands and hundreds of thousands.
Then comes the third grade - million class. It also consists of three categories: seventh, eighth, ninth. It includes millions, tens of millions and hundreds of millions.
The next three categories - the tenth, eleventh and twelfth - form the fourth class - billion class, consisting of units of billions, tens of billions and hundreds of billions.
The next three digits form new class, and so on. The unit of the fifth class is called trillion(1 trillion = 1000 billion). Units of the sixth, seventh, eighth, etc. classes (each 1000 times larger than the previous one) are called, respectively, quadrillion, quintillion, sextillion, septillion, octillion etc.
The selection of classes creates convenience not only for writing, but also for reading numbers. Names are given to the first ten numbers, and then, using a small set of new words and decimal notation, the names of the following numbers are formed.
The names of the numbers of the second ten are formed from the combination of the first ten names and the word twenty(from the word ten): eleven - one in ten; twelve - two by ten; thirteen - three times ten, etc. Word twenty stands for two tens.
The names of the third ten numbers are formed from the word twenty and the names of the numbers of the first ten: twenty-one, twenty-two, twenty-three, etc.
The names of the numbers of the fourth, fifth, sixth, seventh, eighth, ninth and tenth tens are formed according to the same rule, but with the addition of three new words: forty, ninety and one hundred.
The names of the numbers of the second hundred are made up of the word one hundred and the names of the numbers of the first hundred: one hundred and one, one hundred and two, etc., one hundred ninety-nine. Two hundred is briefly called two hundred.
The subsequent hundreds are counted in the same way. Three hundred - three hundred, four hundred - four hundred, five hundred - five hundred etc. up to ten hundred. A new word is used for ten hundred thousand. A thousand thousand has a special name million. A thousand million is called billion(or billion).
For the name of all natural numbers within a billion, only 16 different words turned out to be enough: one, two, three, four, five, six, seven, eight, nine, ten, forty, ninety, one hundred, one thousand, one million, one billion. These words are the main ones, and all the names of the remaining numbers up to a billion are obtained from them according to the rules described above.
Decimal notation of numbers makes it quite easy to solve issues related to comparing natural numbers, as well as their addition, subtraction, multiplication and division. Since all these operations are studied in the elementary course of mathematics, let us dwell on their theoretical justification in more detail.
2. The algorithm for comparing natural numbers follows from the following theorem.
Theorem 2. Let natural numbers X And at written in decimal notation:
Number x less than number at if one of the following conditions is met:
A) P< m;
b) n = t, But A P < b P ;
V) n =m, A P = b b , ..., A i = b i, But A i -1 < b i -1 .
Proof. a) Let P< т.
It means that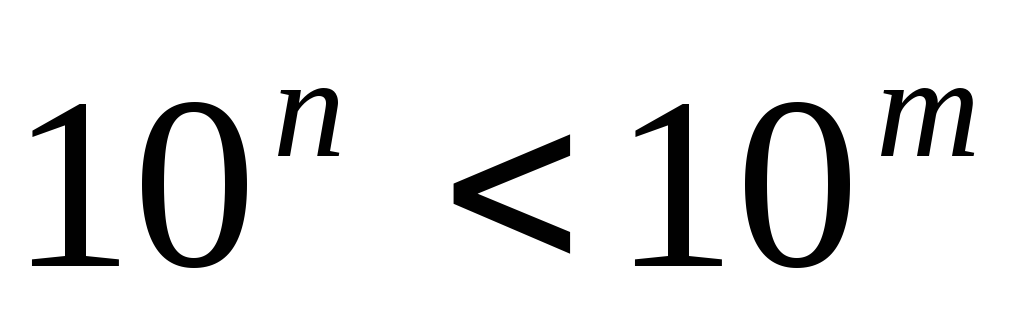 
, or 
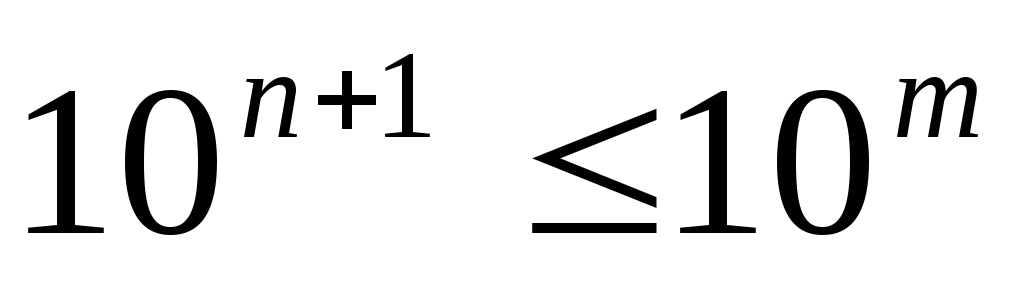. Besides, X<
10 n+1 and y ≥ 10 m. Then we have a chain of inequalities X<
10 n +1
≤ 10 m
≤ y, from which it follows that X< у.
b) Let n =m, But A P
<
b P .
Then A P
+
1 ≤ b n. Multiplying both parts of the last inequality by 10 P, we get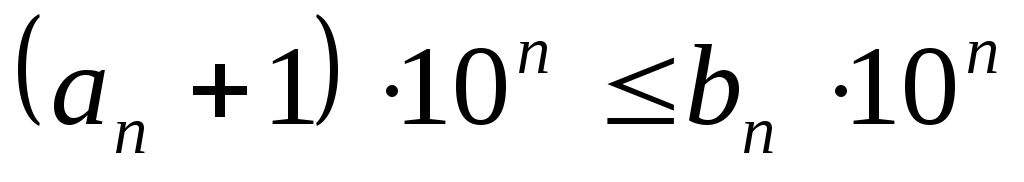 
. Besides, 
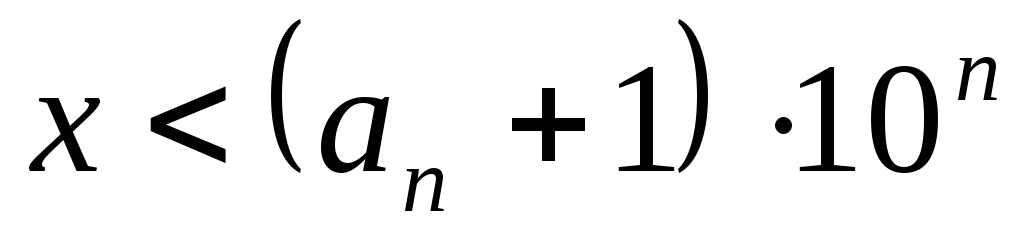And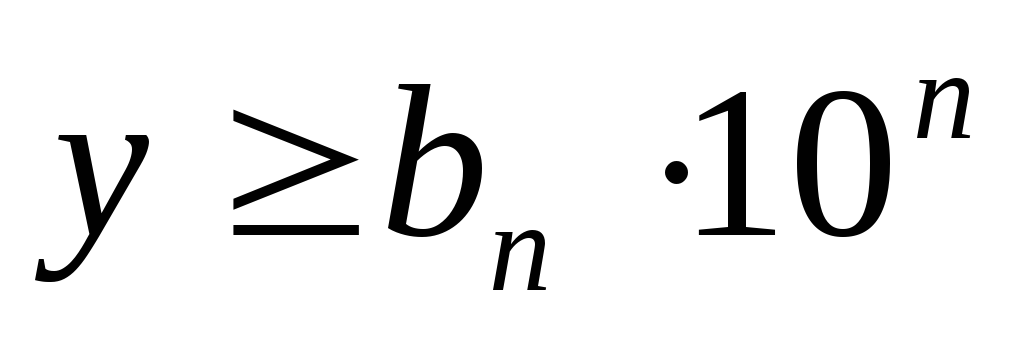 
. Therefore, we can write down a chain of inequalities, which again implies that X< у
.
The proof of the theorem for case c) is carried out in a similar way.
3. Let's derive an algorithm for adding multi-digit numbers in the decimal number system. First, consider the case when the number of digits in the notation of numbers X And at equally. Let
Then, applying the commutative and associative laws of addition, as well as the distributive law of multiplication with respect to addition, we can write:
The last formula cannot be considered as a decimal representation of a number x + y, since the coefficients 
(i
= 0, 1, 2, …, n) can be greater than 9, which means that the addition operation cannot be considered complete. To complete the addition, choose the smallest number i, for which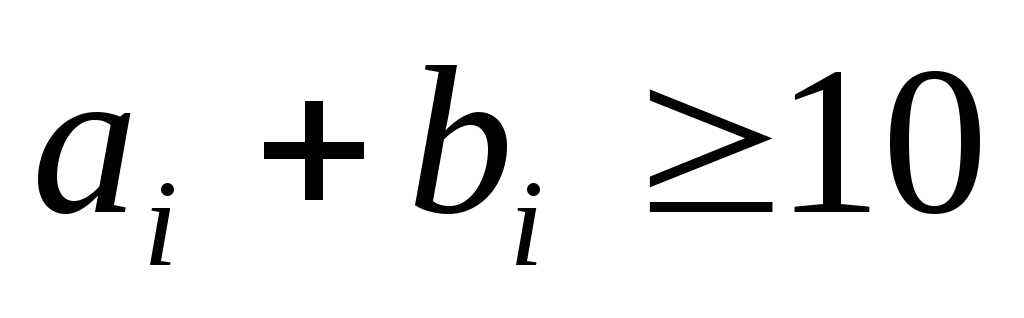 
. From the fact that 0 ≤ A i≤ 9 and 0 ≤ b i≤ 9, the inequality 0 ≤ A i
+
b i
≤ 18.
This means that the amount can always be represented as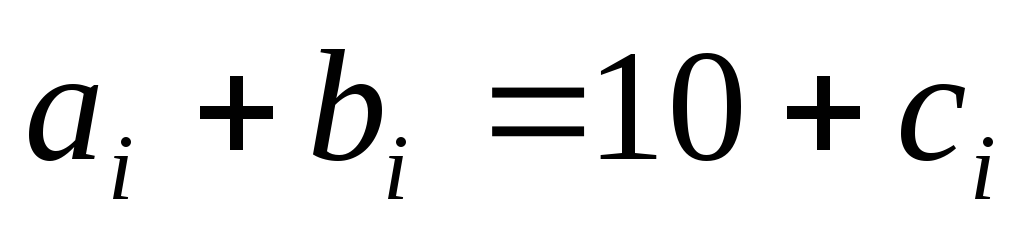 
, where 0 ≤ With i≤ 9. Then , and hence, in equality (9) the terms can be replaced by .
After that, we consider the coefficients . Denote by j the smallest number for which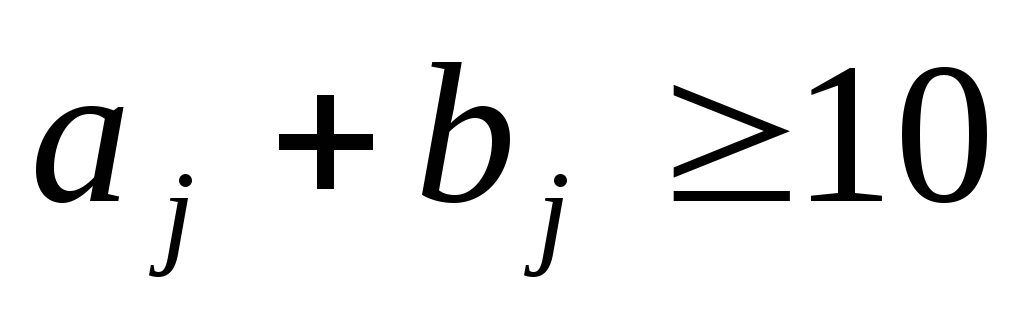 
(j
= i
+ 1, i
+ 2,..., n) and repeat the above procedure. Continuing this process, no more than P steps, we arrive at one of the equalities:
each of which is a decimal representation of a natural number x + y.
The general case, when the decimal notation of numbers has a different number of characters, is easily reduced to the one considered by adding the required number of zeros in front of the number.
From the described process follows
Addition algorithm multivalued natural numbers represented in the decimal number system.
1. We write the second term under the first so that the corresponding digits are one under the other.
2. We add single-digit numbers of the discharge of units. If their sum is less than ten, then we write it in the category of units of the answer and move on to the next category (tens).
3. If the amount single digits in the unit digit is greater than or equal to 10, then we represent it as 10 + With 0 , where With 0 - a single digit, then write With 0 to the units of the answer and add one to the number of tens.
4. We repeat the same actions with tens, then with hundreds, etc. The process ends when the single-digit numbers of the highest digits are added.
4. Let two numbers be given X And at:
Where y < x. Using the properties of the subtraction operation, we can write:
If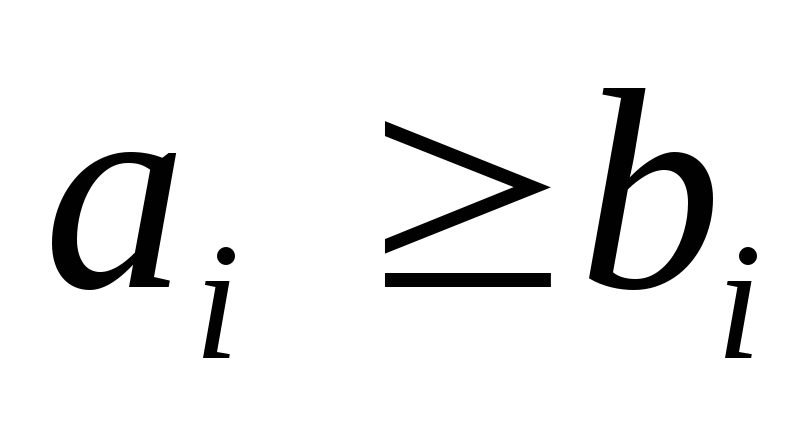 
(i
= 0, 1, 2, …, n), then the last equality specifies the subtraction algorithm.
If 
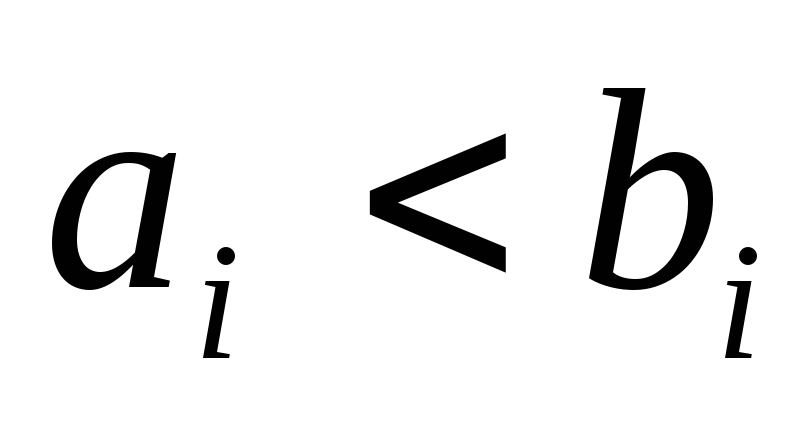for some rooms i, then we take the least i for which this condition is satisfied. Moreover, suppose that , but 
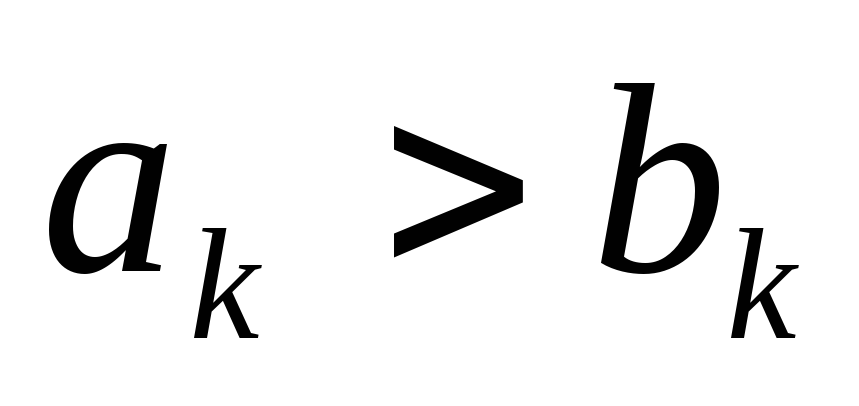(k
>
i). Next, we use the equation:
The validity of equality (11) is easily established by reducing the right side to the left side.
Using equality (11), representation (10) of the difference x – y can be rewritten in the following form:
In the last equality, all coefficients with an index less than k (we will refer to them c j , j = k – 1, …, 1, 0), with corresponding powers of 10, satisfy the inequalities: 0 ≤ With j ≤ 9, j = k – 1, ...,1, 0.
Applying similar transformations to coefficients with numbers greater than or equal to k, through P steps, we arrive at equality (10) in the form:
0 ≤ With i ≤ 9, i = 0, 1, ..., P.
It follows from the above
Subtraction algorithm multivalued natural numbers represented in the decimal number system.
1. We write the subtracted under the reduced so that the corresponding digits are one under the other.
2. We start the subtraction with the unit digit. If the number in the units place of the subtrahend does not exceed the number in the units place of the minuend, then we subtract, and then move on to the next digit.
3. If the number in the ones place of the subtrahend exceeds the number in the units place of the minuend, then we occupy the unit in the tens place, thereby increasing the number of units by 10. After that, we subtract and move on to the next category.
4. If in the category of tens, hundreds, etc. zeros are written in the reduced, then we occupy a unit in the first, non-zero, digit of the reduced, thereby increasing all the lower digits to ones by 9, and the number of the units digit by 10. After that, we subtract and move on to the next digit.
5. In the next category, we repeat the described process.
6. The subtraction process ends when the subtraction from the highest digit of the reduced one is made.
5.
We will divide the derivation of the multiplication rule for multi-digit natural numbers written in the decimal number system into several stages: multiplication of a multi-digit number by a single one; multiplication of a multi-digit number by numbers of the form 10 k; multiplication of a multi-digit number by numbers of the form
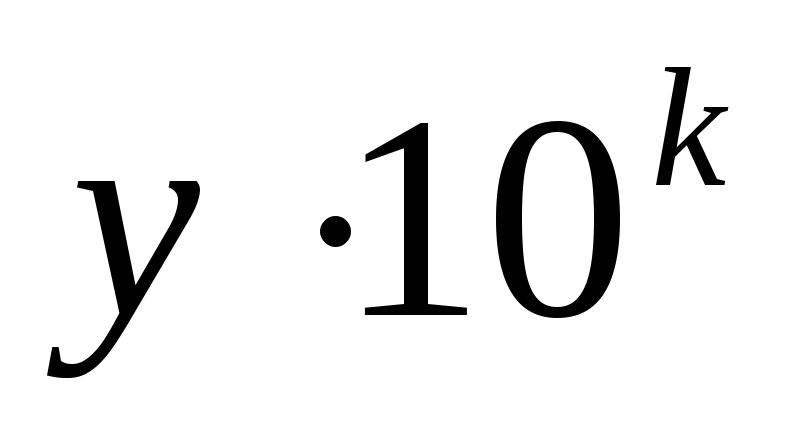, Where at- single digit; Multiplication of a multi-digit number by a multi-digit number. Let's consider each of these steps in turn. Let
And at- single digit. Then
Now, using the multiplication table, we will replace all products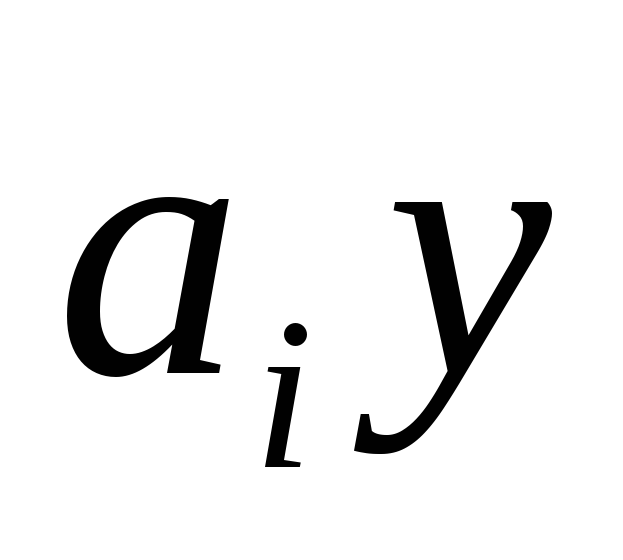 
(i
=
0,
1, ..., P) in the last equality by the corresponding values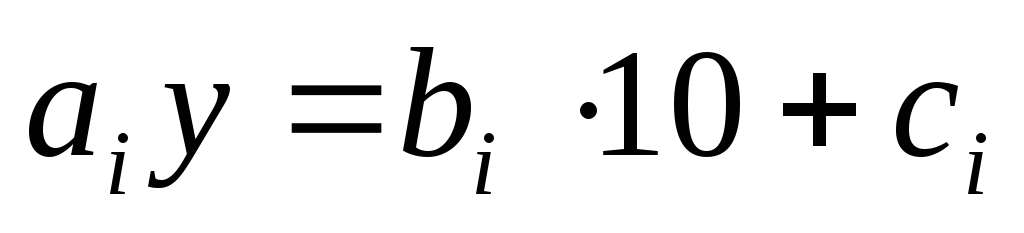 
, where 0 ≤ With i≤ 9. As a result, we obtain the equality:
If in the last expression all sums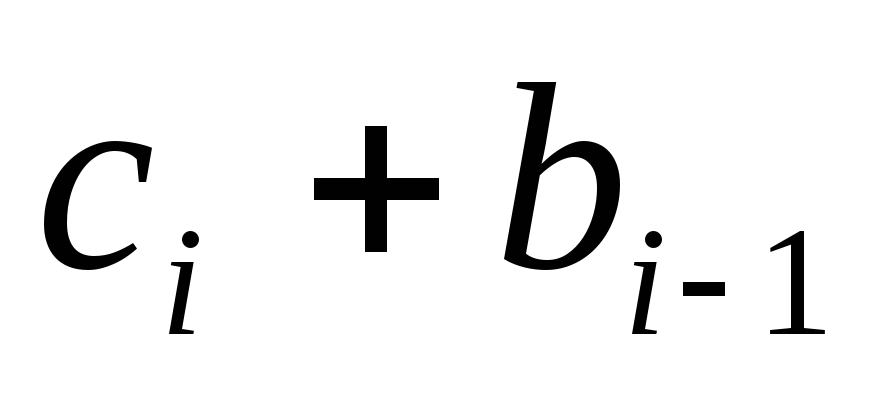 
(i
=
0,
1, ..., P) satisfy the condition 0 ≤ With i
+ b i
≤ 9, then it can be considered a decimal representation of the number x y. If, however, the inequalities hold for some sums With i
+ b i≥ 10, then, representing them in the form With i
+ b i
=
10
+ d i, where 0 ≤ d i≤ 9, writing d i
in the corresponding digit and adding one to the next digit, we get the decimal notation for the number x y.
Let us show that multiplication by numbers of the form 10 k boils down to assigning k zeros to decimal notation X.
Really,
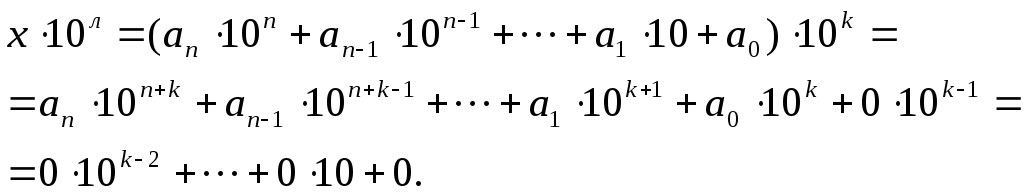
The last expression is the decimal representation of the number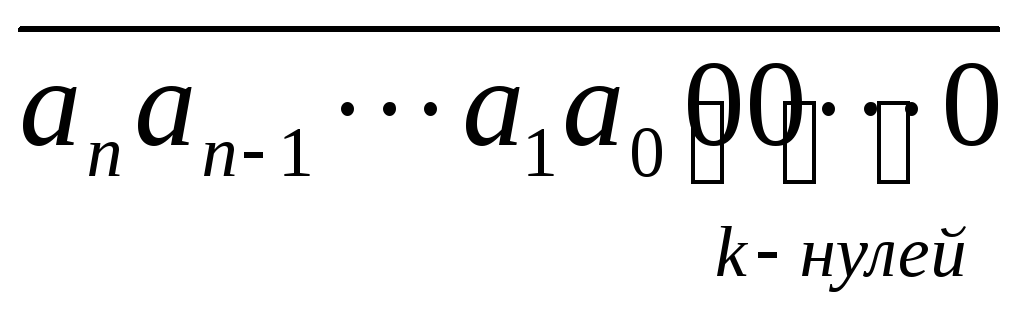 
.
Considering multiplication multi-digit numbers on numbers of the form 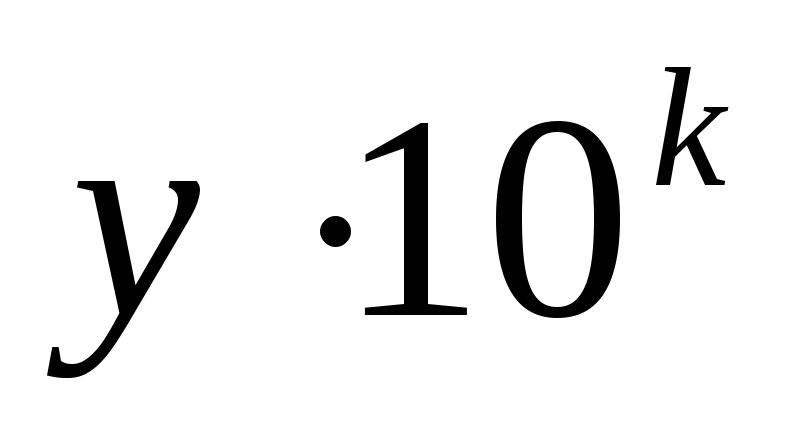, Where y - single-digit number, note that multiplication reduces to successive multiplication by a single-digit number at and on the number 10 k. Both of these methods are described above.
Let us now dwell on the multiplication of a multi-digit number by a multi-digit number. Let X And y - multiple digits and
Using the distributive law of multiplication with respect to addition, as well as the associative law of multiplication of non-negative integers, we can write:
From the last equality, it is obvious that the multiplication of a multi-digit number by a multi-digit number is reduced to the successive multiplication of a multi-digit number X to single digits b m , b m -1 , …, b 1 , b 0 , and then - to the numbers 10 m , 10 m-1 , ..., 10, 1. As a result, we get the terms, the sum of which is the decimal representation of the number x y.
In general
Multiplication algorithm multi-digit number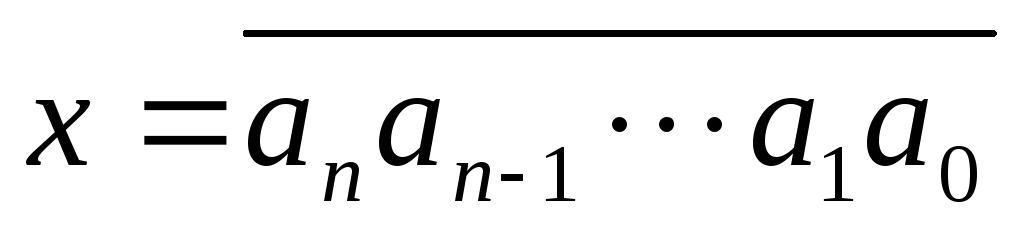 
to a multi-digit number 
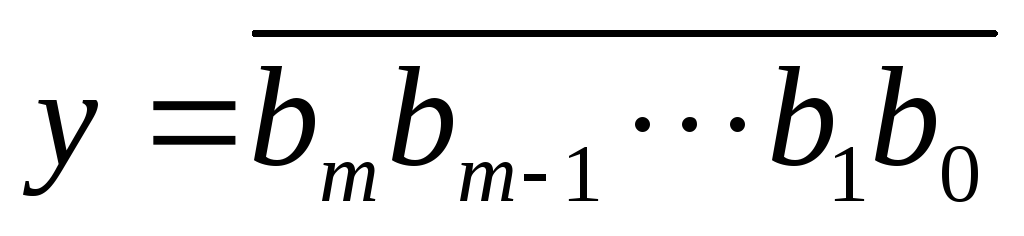can be formulated like this:
1. Write down the multiplier at under the multiplier X.
2. Multiply the number X to a single number b 0 , written in the second digit of the multiplier y. Work X ·b 0 write under the number y.
3. Multiply the number X to a single number b 1 , written in the second digit of the multiplier y. Work X ·b 1 we write in the next line with a shift by one digit to the left, which corresponds to multiplication X ·b 1 on 10.
4. We continue the described process of calculations until the product is calculated X ·b T .
5. Received m+ 1 works add up.
6. Theoretically, the process of dividing a non-negative integer by a natural number relies on division with a remainder. Since the execution of the action of dividing a multi-valued number by a multi-valued number is generally accompanied by cumbersome calculations and the difficulties associated with this, we will consider the derivation of the division algorithm using specific examples.
Consider first division by a single digit. The division of one-digit and two-digit numbers by one-digit is performed using the multiplication table and does not cause labor. Let it be required to divide the three-digit number 356 by 6. Since 60< 356 < 600, то неполное частное q is enclosed between the numbers 10 and 100 and is therefore a two-digit number. Using the multiplication table, you can find more accurate approximations to the number: 356: 6 · 50 < 356 < 6 · 60 или 300 < 356 < 360. Отсюда следует, что неполное частное q concluded between the numbers 50 and 60, that is, it contains 5 tens and has the form q = 5 10+ a 0 . But then the inequality
(50 + A 0) 6 ≤ 356< (50 + A 0 + 1) 6,
Writing numbers in the decimal number system.
Comparison of numbers.
Addition.
Subtraction.
Multiplication.
1. Of all the positional number systems, the decimal system is now widely used. Therefore, we will dwell on writing and reading numbers in this system in more detail.
Definition 2. Decimal notation natural number X is called its representation in the form
where 0 ≤ A i ≤ 9 (i = 0, 1, ..., P), A P ≠ 0.
Numbers 1, 10, 10 2 , 10 3 , ..., 10 P are called here bit units, respectively, the first, second, third, etc. discharges.
The first three digits in the notation of a number are combined into one group and are called the first class, or unit class. The first class includes units, tens and hundreds.
The next three ranks - the fourth, fifth and sixth - form the second class, or thousands class. It includes units of thousands, tens of thousands and hundreds of thousands.
Then comes the third grade - million class. It also consists of three categories: seventh, eighth, ninth. It includes millions, tens of millions and hundreds of millions.
The next three categories - the tenth, eleventh and twelfth - form the fourth class - billion class, consisting of units of billions, tens of billions and hundreds of billions.
The next three digits form a new class, and so on. The unit of the fifth class is called trillion(1 trillion = 1000 billion). Units of the sixth, seventh, eighth, etc. classes (each 1000 times larger than the previous one) are called, respectively, quadrillion, quintillion, sextillion, septillion, octillion etc.
The selection of classes creates convenience not only for writing, but also for reading numbers. Names are given to the first ten numbers, and then, using a small set of new words and decimal notation, the names of the following numbers are formed.
The names of the numbers of the second ten are formed from the combination of the first ten names and the word twenty(from the word ten): eleven - one in ten; twelve - two by ten; thirteen - three times ten, etc. Word twenty stands for two tens.
The names of the third ten numbers are formed from the word twenty and the names of the numbers of the first ten: twenty-one, twenty-two, twenty-three, etc.
The names of the numbers of the fourth, fifth, sixth, seventh, eighth, ninth and tenth tens are formed according to the same rule, but with the addition of three new words: forty, ninety and one hundred.
The names of the numbers of the second hundred are made up of the word one hundred and the names of the numbers of the first hundred: one hundred and one, one hundred and two, etc., one hundred ninety-nine. Two hundred is briefly called two hundred.
The subsequent hundreds are counted in the same way. Three hundred - three hundred, four hundred - four hundred, five hundred - five hundred etc. up to ten hundred. A new word is used for ten hundred thousand. A thousand thousand has a special name million. A thousand million is called billion(or billion).
For the name of all natural numbers within a billion, only 16 different words turned out to be enough: one, two, three, four, five, six, seven, eight, nine, ten, forty, ninety, one hundred, one thousand, one million, one billion. These words are the main ones, and all the names of the remaining numbers up to a billion are obtained from them according to the rules described above.
Decimal notation of numbers makes it quite easy to solve issues related to comparing natural numbers, as well as their addition, subtraction, multiplication and division. Since all these operations are studied in the elementary course of mathematics, let us dwell on their theoretical justification in more detail.
2. The algorithm for comparing natural numbers follows from the following theorem.
Theorem 2. Let natural numbers X And at written in decimal notation:
Number x less than number at if one of the following conditions is met:
A) P< m;
b) n = t, But A P < b P ;
V) n =m, A P = b b , ..., A i = b i, But A i -1 < b i -1 .
Proof. a) Let P< т.
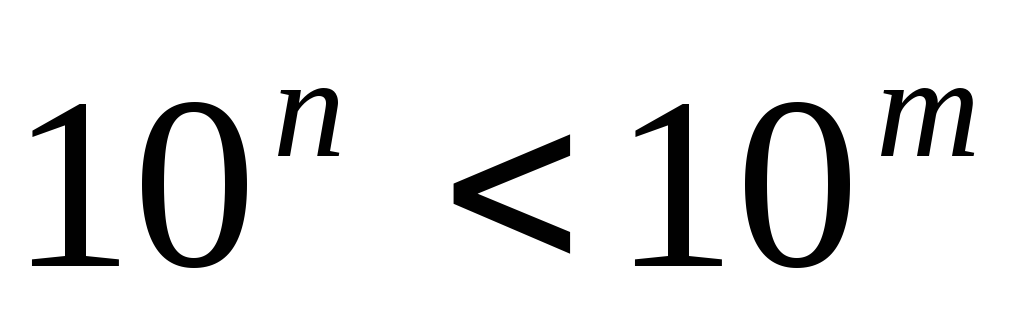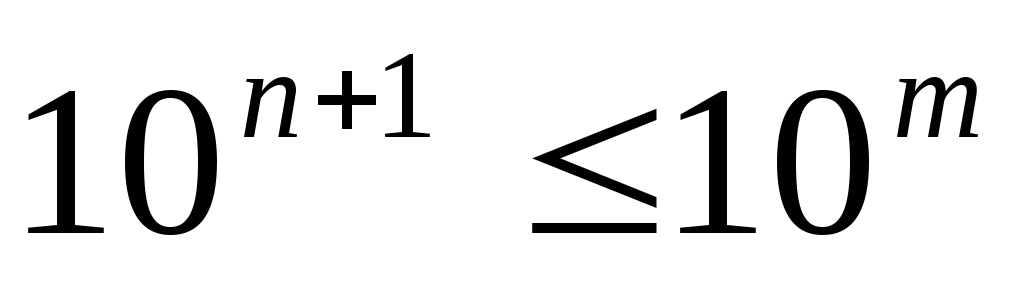It means that , or . Besides, X<
10 n+1 and y ≥ 10 m. Then we have a chain of inequalities X<
10 n +1
≤ 10 m
≤ y, from which it follows that X< у.
b) Let n =m, But A P
<
b P .
Then A P
+
1 ≤ b n. Multiplying both parts of the last inequality by 10 P, we get 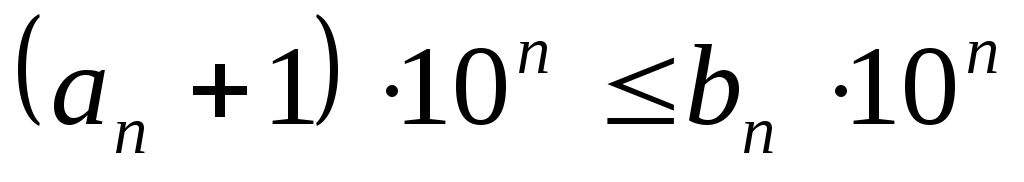. Besides, 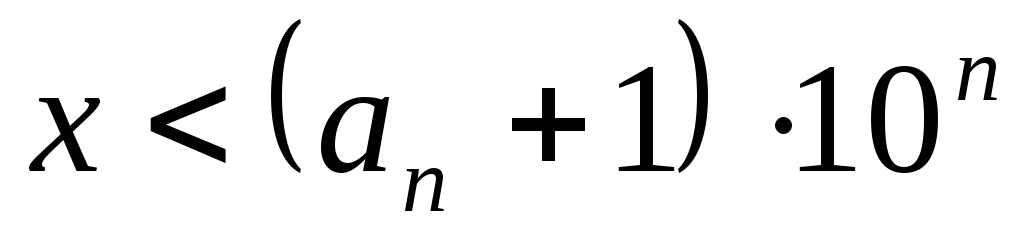And 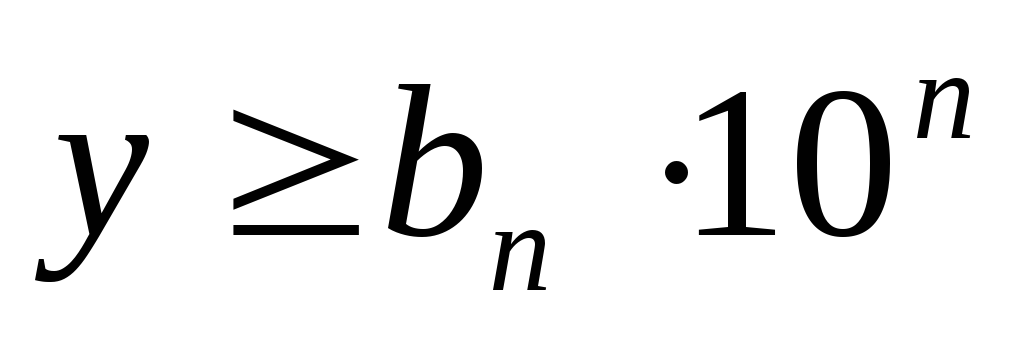. Therefore, we can write down a chain of inequalities, which again implies that X< у
.
The proof of the theorem for case c) is carried out in a similar way.
3. Let's derive an algorithm for adding multi-digit numbers in the decimal number system. First, consider the case when the number of digits in the notation of numbers X And at equally. Let
Then, applying the commutative and associative laws of addition, as well as the distributive law of multiplication with respect to addition, we can write:
The last formula cannot be considered as a decimal representation of a number x + y, since the coefficients (i
= 0, 1, 2, …, n) can be greater than 9, which means that the addition operation cannot be considered complete. To complete the addition, choose the smallest number i, for which 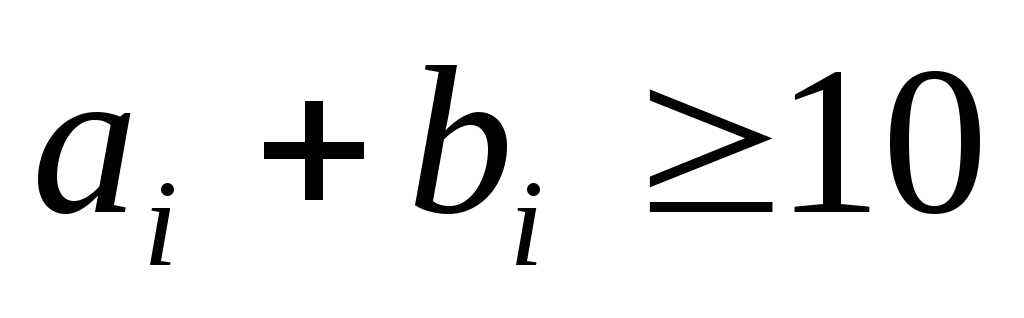. From the fact that 0 ≤ A i≤ 9 and 0 ≤ b i≤ 9, the inequality 0 ≤ A i
+
b i
≤ 18.
This means that the amount can always be represented as 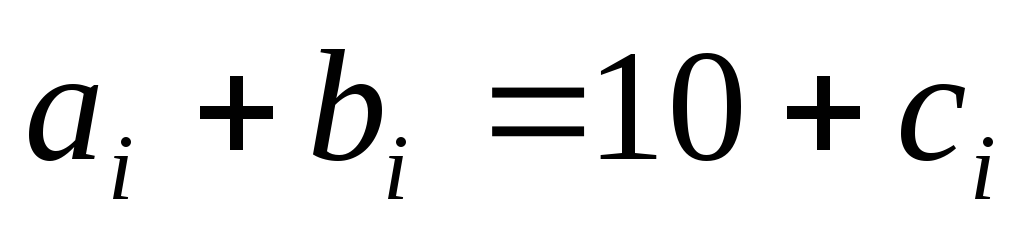, where 0 ≤ With i≤ 9. Then , and hence, in equality (9) the terms can be replaced by .
After that, we consider the coefficients . Denote by j the smallest number for which 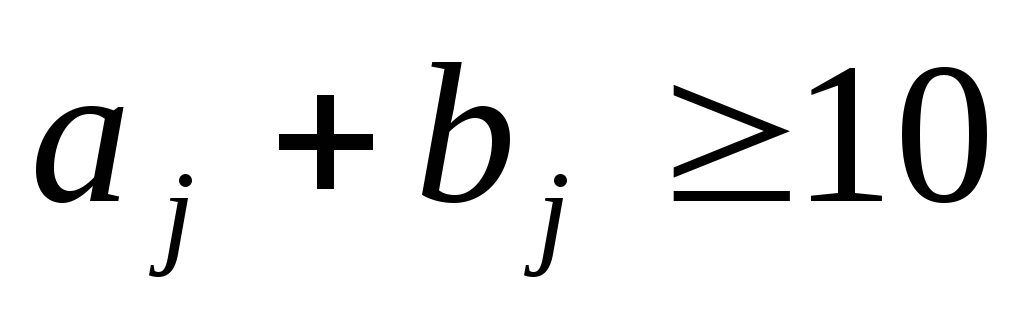(j
= i
+ 1, i
+ 2,..., n) and repeat the above procedure. Continuing this process, no more than P steps, we arrive at one of the equalities:
each of which is a decimal representation of a natural number x + y.
The general case, when the decimal notation of numbers has a different number of characters, is easily reduced to the one considered by adding the required number of zeros in front of the number.
From the described process follows
Addition algorithm multivalued natural numbers represented in the decimal number system.
1. We write the second term under the first so that the corresponding digits are one under the other.
2. We add single-digit numbers of the discharge of units. If their sum is less than ten, then we write it in the category of units of the answer and move on to the next category (tens).
3. If the sum of single-digit numbers in the place of units is greater than or equal to 10, then we represent it in the form 10 + With 0 , where With 0 - a single digit, then write With 0 to the units of the answer and add one to the number of tens.
4. We repeat the same actions with tens, then with hundreds, etc. The process ends when the single-digit numbers of the highest digits are added.
4. Let two numbers be given X And at:
Where y < x. Using the properties of the subtraction operation, we can write:
If 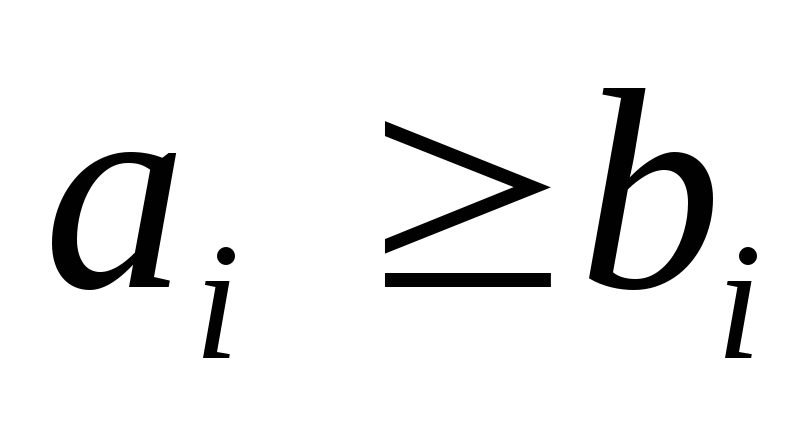(i
= 0, 1, 2, …, n), then the last equality specifies the subtraction algorithm.
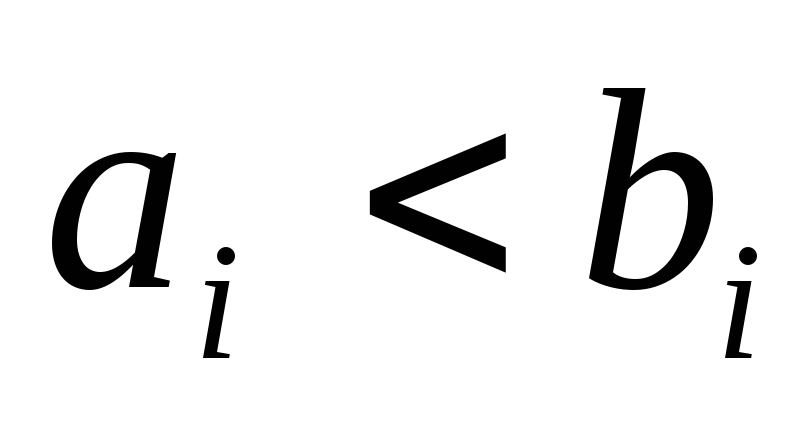If for some rooms i, then we take the least i for which this condition is satisfied. Moreover, suppose that , but 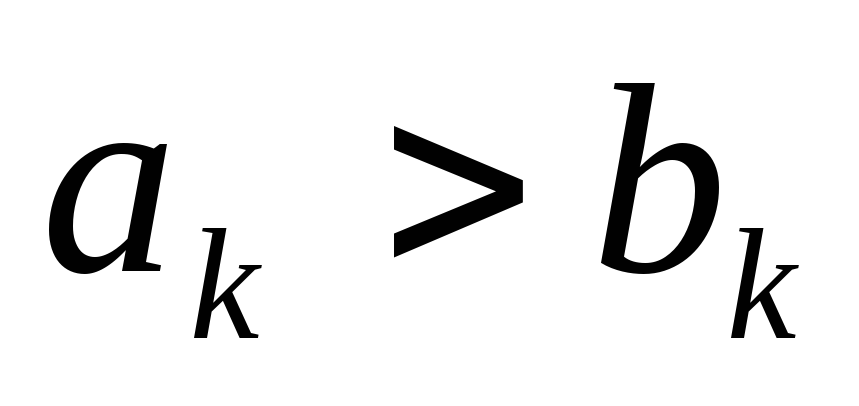(k
>
i). Next, we use the equation:
The validity of equality (11) is easily established by reducing the right side to the left side.
Using equality (11), representation (10) of the difference x – y can be rewritten in the following form:
In the last equality, all coefficients with an index less than k (we will refer to them c j , j = k – 1, …, 1, 0), with corresponding powers of 10, satisfy the inequalities: 0 ≤ With j ≤ 9, j = k – 1, ...,1, 0.
Applying similar transformations to coefficients with numbers greater than or equal to k, through P steps, we arrive at equality (10) in the form:
0 ≤ With i ≤ 9, i = 0, 1, ..., P.
It follows from the above
Subtraction algorithm multivalued natural numbers represented in the decimal number system.
1. We write the subtracted under the reduced so that the corresponding digits are one under the other.
2. We start the subtraction with the unit digit. If the number in the units place of the subtrahend does not exceed the number in the units place of the minuend, then we subtract, and then move on to the next digit.
3. If the number in the ones place of the subtrahend exceeds the number in the units place of the minuend, then we occupy the unit in the tens place, thereby increasing the number of units by 10. After that, we subtract and move on to the next category.
4. If in the category of tens, hundreds, etc. zeros are written in the reduced, then we occupy a unit in the first, non-zero, digit of the reduced, thereby increasing all the lower digits to ones by 9, and the number of the units digit by 10. After that, we subtract and move on to the next digit.
5. In the next category, we repeat the described process.
6. The subtraction process ends when the subtraction from the highest digit of the reduced one is made.
5.
We will divide the derivation of the multiplication rule for multi-digit natural numbers written in the decimal number system into several stages: multiplication of a multi-digit number by a single one; multiplication of a multi-digit number by numbers of the form 10 k; multiplication of a multi-digit number by numbers of the form
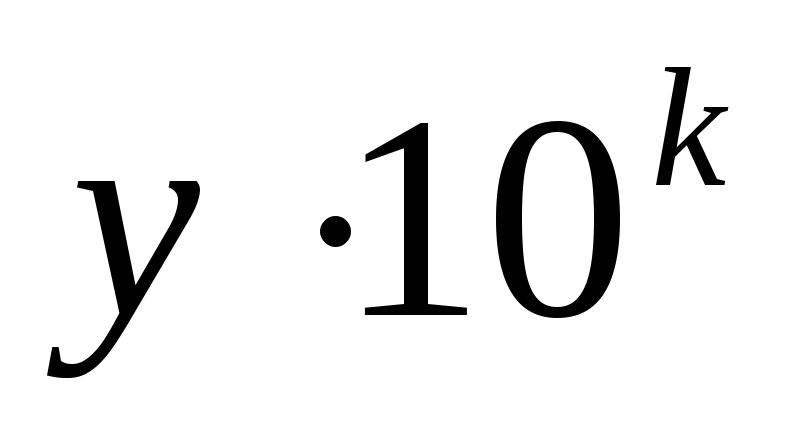, Where at- single digit; Multiplication of a multi-digit number by a multi-digit number. Let's consider each of these steps in turn. Let
And at- single digit. Then
Now, using the multiplication table, we will replace all products 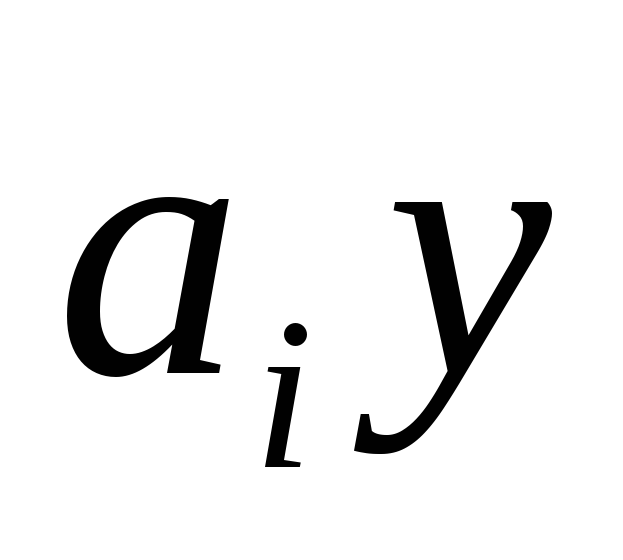(i
=
0,
1, ..., P) in the last equality by the corresponding values 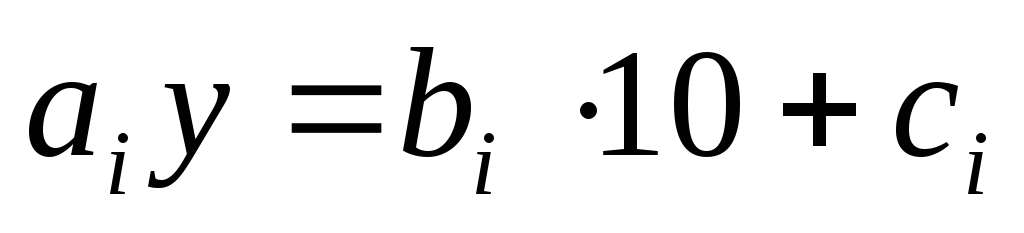, where 0 ≤ With i≤ 9. As a result, we obtain the equality:
If in the last expression all sums 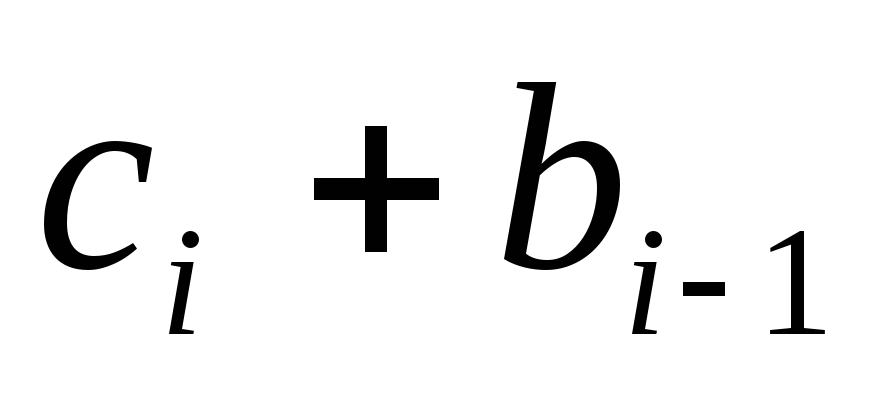(i
=
0,
1, ..., P) satisfy the condition 0 ≤ With i
+ b i
≤ 9, then it can be considered a decimal representation of the number x y. If, however, the inequalities hold for some sums With i
+ b i≥ 10, then, representing them in the form With i
+ b i
=
10
+ d i, where 0 ≤ d i≤ 9, writing d i
in the corresponding digit and adding one to the next digit, we get the decimal notation for the number x y.
Let us show that multiplication by numbers of the form 10 k boils down to assigning k zeros to decimal notation X.
Really,
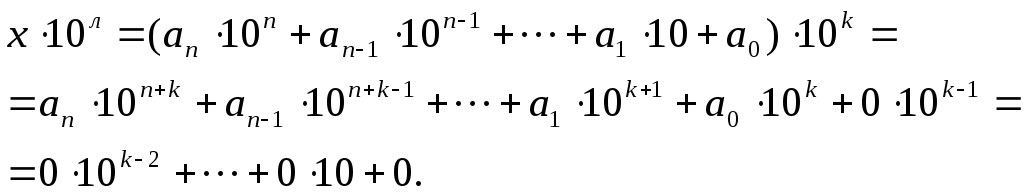
The last expression is the decimal representation of the number .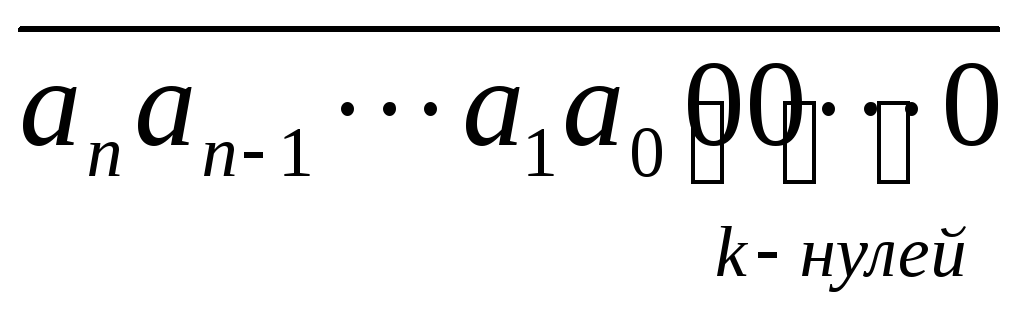
Considering the multiplication of multi-valued numbers by numbers of the form 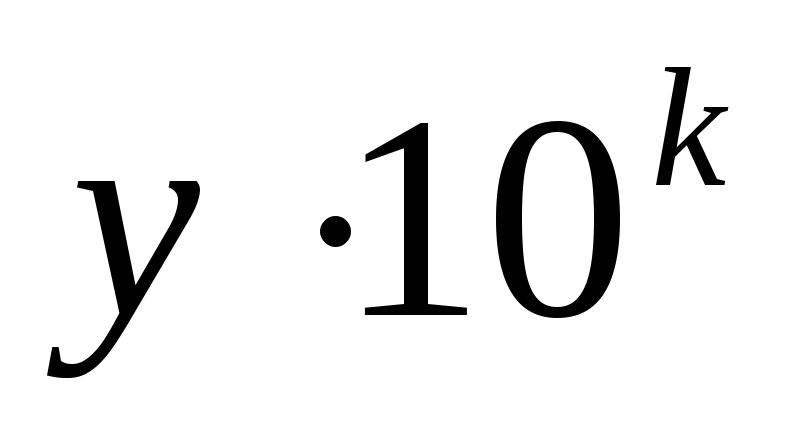, Where y - single-digit number, note that multiplication reduces to successive multiplication by a single-digit number at and on the number 10 k. Both of these methods are described above.
Let us now dwell on the multiplication of a multi-digit number by a multi-digit number. Let X And y - multiple digits and
Using the distributive law of multiplication with respect to addition, as well as the associative law of multiplication of non-negative integers, we can write:
From the last equality, it is obvious that the multiplication of a multi-digit number by a multi-digit number is reduced to the successive multiplication of a multi-digit number X to single digits b m , b m -1 , …, b 1 , b 0 , and then - to the numbers 10 m , 10 m-1 , ..., 10, 1. As a result, we get the terms, the sum of which is the decimal representation of the number x y.
In general
Multiplication algorithm multi-digit number 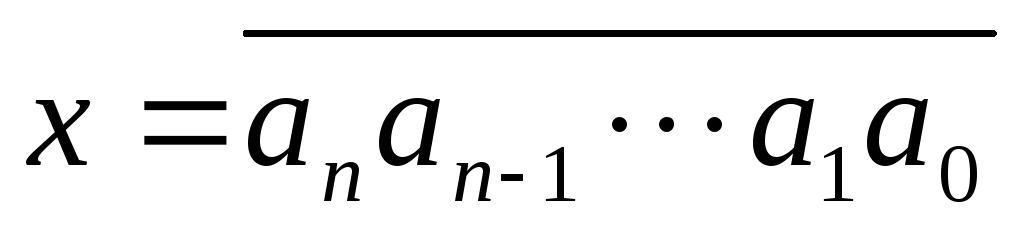to a multi-digit number 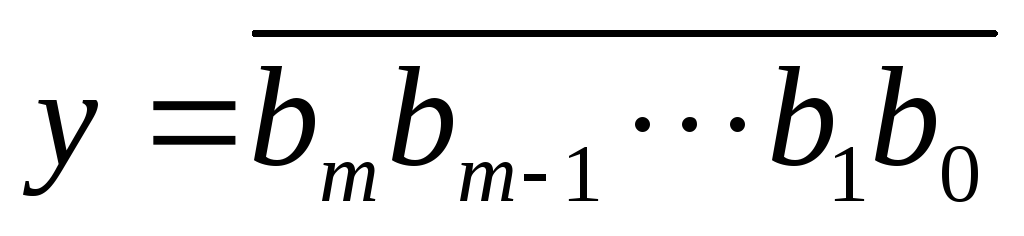can be formulated like this:
1. Write down the multiplier at under the multiplier X.
2. Multiply the number X to a single number b 0 , written in the second digit of the multiplier y. Work X ·b 0 write under the number y.
3. Multiply the number X to a single number b 1 , written in the second digit of the multiplier y. Work X ·b 1 we write in the next line with a shift by one digit to the left, which corresponds to multiplication X ·b 1 on 10.
4. We continue the described process of calculations until the product is calculated X ·b T .
5. Received m+ 1 works add up.
6. Theoretically, the process of dividing a non-negative integer by a natural number relies on division with a remainder. Since the execution of the action of dividing a multi-valued number by a multi-valued number is generally accompanied by cumbersome calculations and the difficulties associated with this, we will consider the derivation of the division algorithm using specific examples.
Consider first division by a single digit. The division of one-digit and two-digit numbers by one-digit is performed using the multiplication table and does not cause labor. Let it be required to divide the three-digit number 356 by 6. Since 60< 356 < 600, то неполное частное q is enclosed between the numbers 10 and 100 and is therefore a two-digit number. Using the multiplication table, you can find more accurate approximations to the number: 356: 6 · 50 < 356 < 6 · 60 или 300 < 356 < 360. Отсюда следует, что неполное частное q concluded between the numbers 50 and 60, that is, it contains 5 tens and has the form q = 5 10+ a 0 . But then the inequality
(50 + A 0) 6 ≤ 356< (50 + A 0 + 1) 6,
Lesson topic: Number systems. Translation of numbers.
Lesson objectives:the formation of knowledge about the emergence and development of ways to write integer non-negative numbers; formation of knowledge about how to write numbers and the ability to apply translation rules in various positional number systems, including using non-standard tasks; development of skills to analyze, compare; education of the ability to listen and analyze the response of a fellow student, the ability to overcome cognitive difficulties.
Equipment: presentation "History of the number system" (prepared by students), presentation "Number systems", "Test", multimedia projector, handout: table "Powers of number: 2; 8; 16", "Number system". Lesson plan
1. Organizational moment.
Epigraph: "Everything is a number" - said the Pythagoreans.
Every day we deal with different number systems: 60 is a number system for measuring time, 24 is the number of hours in a day, 7 is the days of the week, 12 is months, 2 is a computer number system, 10 is Arabic numerals, etc.; We are surrounded by many...
Communication of the objectives of the lesson.
A modern person in everyday life is constantly faced with numbers: we memorize bus and phone numbers, calculate the cost of purchases in a store, and manage our family budget. Numbers, figures... they are with us everywhere. And what did a person know about numbers several thousand years ago?
Student messages: "History of number systems."
3. Explanation of new material
To write numbers, mankind mainly uses the decimal number system.
What is a number system?
Notation is a way of writing numbers using special characters - numbers.
Number system: gives representations of a set of numbers; gives each number a unique representation (or at least a standard representation); reflects the algebraic and arithmetic structure of numbers. The language of numbers, like any other, has its own alphabet.
Numbers: 123, 45678, 1010011, CXL
Numbers:- characters used to write a number. 0, 1, 2, … I, V, X, L, …
Discharge- the position of the digit in the number
5 4 3 2 1 0 digit
9 5 6 7 8 4
Alphabet is a set of numbers. (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
Radix is the number of digits used in this number system.
Number system basis is the sequence of base degrees.
10SS: 10^n,10^n-1,...,10^5,10^4, 10^3 10^2,10^1,10^0
2CC: 2^n,2^n-1,...,2^5,2^4, 2^3,2^2,2^1,2^0
8CC: 8^n,8^n-1,...,8^5,8^4, 8^3 ,8^2.8^1.8^0
16CC: 16^n,16^n-1,...,16^5,16^4, 16^3,16^2,16^1,16^0
Types of number systems: positional, non-positional.
The most common in the XXI century are positional number systems.
positional- the value of a digit depends on its place (position) in the notation of the number.
Positional: sexagesimal, binary, hexadecimal, decimal...
In the number 555, the first 5 is in the position of hundreds, the second 5 is in the position of tens, the third 5 is in the position of one (555=500+50+5).
In programming, positional systems with base 8 and 16 are widely used. In the octal number system, 8 digits are used - 0,1,2,3,4,5,6,7. In the hexadecimal number system, the missing numbers are replaced by letters of the Latin alphabet: A \u003d 10,B=11,C=12,D=13,E=14,F=15.
non-positional- the value of a digit does not depend on its place (position) in the notation of the number.
Non-positional: Single (unary) system, Roman system, Ancient Egyptian decimal system, alphabetical number system.
Roman numeral system
I V X L C D M
1 5 10 50 100 500 1000
Algorithm for transferring from 10CC to other positional number systems:
Divide a decimal number by the base of the number system. Get the quotient and the remainder.
Keep dividing until the last quotient is less than the base of the new number system.
Write the last quotient and all remainders in reverse order. The resulting number will be a record in the new number system.
121(10SS) = 1111001(2SS)
571(10SS) = 1073(8SS)
7467(10SS) = 1 13 2 11(16SS)= 1D2B(16SS)
Algorithm for converting numbers from any number system to decimal.
Write this number in general form:
ABCP=A p^2+B p^1+C p^0
Find the sum of the series. The resulting number is the value of the number in 10CC.
10011(2SS)=1 2^4+0 2^3+0 2^2+1 2^1+1 2^0=19(10SS)
144(8SS)=1 8^2+4 8^1+4 8^0=64+32+4=100(10SS)
1C5(16CC)=1 8^2+4 8^1+4 8^0=64+32+4=453(10CC)
Translation from 2SSv 8SS.
We divide this number into triads (into groups of three digits). According to the table, we look at the correspondence between binary and octal number systems.
1 100 101 011=1453
Translation from 2SSv 16SS.
We divide this number into tetrads (into groups of four digits). According to the table, we look at the correspondence between binary and hexadecimal number systems.
11 0010 1011=32V
Operations with numbers.
Example. Let p = 5. Calculate 3445 + 2425.
Solution.
1) 4 + 2 = 6 = 11
one of the terms.
2) 4 + 4 +1 = 9 = 14: 4 is written to the result and one "hundred" is added to the "hundreds"
one of the terms.
3).3 + 2 + 1 =6 = 11: write to the result.
We get: 344 + 242 = 1141.
Example. p = 2
10110 +111011=1010001
Example.p = 2
110111+101101=1100100
4. Fixing the new material.
Exercise.
Translate:
A) 10,000 (2SS in 10SS)
B)110010(2cc to 10cc)
C)3710 (8SS to 10SS)
D)151 (16SS in 10SS)
Exercise.
Find the amount:
101101+11111; 10111+101110.
Exercise.
Read a comic poem by A. N. Starikov “An Extraordinary Girl” and try to solve the riddle of the poet. To do this, write down the numbers mentioned in the poem and translate them into the decimal number system.
She was a thousand and a hundred years old
She went to the one hundred and first class,
In a portfolio of a hundred books she carried -
All this is true, not nonsense.
When, dusting with a dozen feet,
She walked along the road
She was always followed by a puppy
With one tail, but hundred-legged.
She caught every sound
With ten ears
And ten tanned hands
They held a briefcase and a leash.
And ten dark blue eyes
Considered the world habitually ...
But everything will become quite normal
When you understand our story.
Exercise.
In which number system is the equation 10 + 10 = 10 10 correct?
5.Knowledge control.Test.
1. In what number system is information stored in a computer presented?
A.in ternary B.in decimal C.in binary D.in duodecimal
2. The advantage of the binary number system is that:
A. binary code saves computer memory
B. electronic elements with two states are the simplest in design
B. Bi-state electronic components consume less electricity
D.binary code does not cause computer crash
3. Octal number system is different from hexadecimal:
A. number of operations on a number per second B. nesting depth of operations
C. the number of digits used to write the number D. the degree of computerization
4. How many digits are used in the ternary number system?
A.3 B.11 C.10 D.2
5. In the hexadecimal number system, the symbol F is used to denote:
A.end of file B.number 16 C.end of line D.number 15
6. Convert from binary to decimal number 101010101
A.361 B.564 C.455 D.341
7. Convert from decimal to binary number 216
A.11001100 B.11011000 C.11100000 D.11001000
6. Summing up the lesson.
Frontal survey on new material:
What is a number system?
What number systems are called positional?
What number systems are called non-positional?
Explain the algorithm for converting numbers from binary to decimal.
Explain the algorithm for converting numbers from decimal to binary.
Explain the algorithm for converting numbers from any positional system to decimal.
Explain the algorithm for converting numbers from the decimal system to any other positional system.
7. Reflection.
8. Homework.
1. Transfer from 2 systems to 10CC: 111010011; 100011101; 1110111001
2. Convert from 10 SS to 2SS, 8SS and 16SS the following numbers: 168, 1042, 1517.
3. Write down the numbers given in 2SS in 8SS: (111001101); (101010101).
4. Encode any popular expression using the representation of the numbers of letters of the Russian alphabet in various number systems.
Literature:
1.Ch. edited by E. Khlebalin, Universal School Encyclopedia, Avanta +, Moscow, 2003
2. Berman N.G. "Count and number". OGIZ, Moscow 1947.
3. Kagan B.M. Electronic computers and systems, M.: Energoatomizdat, 1985.
4. Fomin S.V. Number systems, M.: Nauka, 1987.
As you know, in the decimal number system, 10 characters (numbers) are used to write numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. From them, final sequences are formed, which are short records of numbers. For example, the sequence 3745 is a shorthand notation for the number 3 × 10 3 + 7 × 10 2 + 4 × 10 + 5.
Definition. The decimal representation of a natural number x is its representation in the form: x \u003d a n 10 n + a n -1 10 n -1 + ... + a 1 10 + a 0, where the coefficients are a n, a n -1, .... , a 1, a 0, take the values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and a p ± 0.
The sum a n 10 n + a n-1 10 n-1 + ... + a 1 10 + a 0 in short form is usually written as follows:
a p a n-1 ...a 1 a 0 .
Since the concept of a number and its notation are not identical, the existence and uniqueness of the decimal notation of a natural number must be proved.
Theorem. Any natural number X can be represented as:
x= , where the coefficients a n , a n -1, …. , a 1, a 0, take the values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and a n ± 0, and such a notation is unique.
Proof of the existence of a number entry X in the form (1). Among the consecutive numbers 1, 10, 10 2 , 10 3 ,..., 10",... find the largest power contained in X, those. such that 10 n< X< 10 n +1 , which can always be done.
Divide (with a remainder) a number X by 10n. If the quotient of these numbers is denoted by a n , and the remainder by x p, That X= a n 10 n + x n, where a n< 10 и х п < 10 n . Next, dividing x n by 10 n -1 , we get: x n= a n -1 10 n -1 + x n -1 where x \u003d a n 10 n + a n -1 10 n -1 + x n -1
Where a n-1< 10 и х n -1 < 10 n -1 . Continuing the division, we reach the equality x 2 \u003d a 1 10 + x 1. Putting x 1 = a 0, will have x \u003d a n 10 n + a n -1 10 n -1 + ... + a 1 10 + a 0, i.e. number X will be represented as the sum of powers of the number 10 with coefficients less than 10, which means that the number can be written X in decimal number system.
Proof of the uniqueness of the representation of a number X in the form (1). Number P in equality (1) is uniquely determined by the condition 10 n< X< 10n+1 . After P defined, coefficient a p found from the condition: a n 10 n< х < (а п + 1) ·10 n . Next, the coefficients a n-1, …. , and 1, and 0 .
The decimal notation of a number allows you to simply decide which one is less.
Theorem. Let X And y - natural numbers, the record of which is given in the decimal number system:
x= a n 10 n + a n -1 10 n -1 + ... + a 1 10 + a 0 ,
at= ,
Then x is less than y, if one of the conditions is met:
A) P< т;
b) p \u003d t, but a p< b п
c) n \u003d t, and n=b p... ,a k = b k, But and k -1 .,< b к -1/
The proof is not given.
For example, if X= 345, and at= 4678, then x< у, так как первое число трехзначное, а второе - четырехзначное. Если X= 345, and y= 467 then x< y, since in the first of two three-digit numbers less than hundreds. If x = 3456 and y= 3467 then X< у, because, despite the fact that in each of four-digit numbers the number of thousands and hundreds is the same, tens in the number X less than in number y.
If a natural number X represented as x= a n 10 n + a n -1 10 n -1 + ... + a 1 10 + a 0, then the numbers 1, 10, 10 2 , ..., 10 n called bit units respectively the first, second, ..., P+ 1 digit, and 10 units of one digit make up one unit of the next highest rank, i.e. the ratio of adjacent digits is equal to 10 - the base of the number system.
The first three digits in the number entry are combined into one group and called first class or class of units. The first class includes units, tens and hundreds.
The fourth, fifth and sixth digits in the number form form second class - thousands class. It includes units of thousands, tens of thousands and hundreds of thousands.
Then follows third class - the class of millions, which also consists of three categories: the seventh, eighth and ninth, i.e. from units of millions, tens of millions and hundreds of millions.
The next three digits also form a new class, and so on. Separation of classes of units, thousands, millions, etc. creates convenience for writing and reading numbers.
In the decimal system, all numbers can be given a name (name). This is comprehended as follows: there are names of the first ten numbers, then from them, in accordance with the definition of decimal notation, and by adding a few more words, the names of subsequent numbers are formed. So, the numbers of the second ten (they are represented as
1∙10 + a 0 are formed from the combination of the first ten names and a slightly modified word ten (“twenty”): eleven - one in ten twelve - two by ten, and so on.
Perhaps it would be more natural to say "two and ten", but our ancestors preferred to say "two by ten", which was preserved in speech.
The word "twenty" means two tens.
Numbers of the third ten (these are numbers of the form 2∙10 + a 0) are obtained by adding the names of the first ten numbers to the word "twenty": twenty-one, twenty-two, etc.
Continuing the count further, we get the name of the numbers of the fourth, fifth, sixth, seventh, eighth, ninth and tenth tens. The names of these numbers are formed in the same way as within the third ten, only in three cases new words appear: forty (to denote four tens), ninety (to denote nine tens) and one hundred (to denote ten tens). The names of the numbers of the second hundred are made up of the word "hundred" and the names of the numbers of the first and subsequent tens. Names are formed in this way: one hundred and one, one hundred and two, ..., one hundred and twenty, etc. Having counted a new hundred, we will have two hundred, which for brevity are called "two hundred". To obtain numbers greater than two hundred, we again use the names of the numbers of the first and subsequent dozens, attaching them to the word "two hundred". Then we get special names: three hundred, four hundred, five hundred, etc. until we count ten hundred, which are called thousand.
Counting beyond a thousand is carried out as follows: adding one thousand to a thousand (one thousand, two thousand, etc.), we get two thousand, three thousand, etc. When we count a thousand thousand, this number will receive a special name - million. Then we count in millions until we reach a thousand million. The resulting new number - a thousand million - has a special name billion, or billion. In calculations, it is customary to write a million as 10 6, a billion - 10 9. By analogy, you can get records big numbers: trillion - 10 12, quadrillion- 10 15 etc.
Thus, in order to name all natural numbers within a billion, it took only 16 different words: one, two, three, four, five, six, seven, eight, nine, ten, forty, ninety, one hundred, one thousand, one million, billion. The remaining names of numbers (within a billion) are formed from the main ones.
The questions of naming and writing numbers are considered in the elementary course of mathematics in the "Numbering" section. In this case, the decimal notation of a natural number is its representation in the form of a sum of digit terms. For example, 3000 + 700 + 40 + 5 is the sum of the bit terms of the number 3745. Representing a number in the form of such sums is convenient for its name: three thousand seven hundred forty-five.
Exercises
1. Write the number as the sum of bit terms:
a) 4725; 6)3370; c) 10255.
2. What numbers are represented by the following amounts:
a) 6∙10 3 + 5∙10 + 8; b) 7∙10 3 + 1 ∙ 10;
c) 8∙10 4 + 10 3 +3∙10 + 1; d) 10 5 + 10 2 ?
3. Write the largest three-digit and ten-digit number in which all digits are different.
4. Solve the problems from the initial course of mathematics using the arithmetic method:
a) The sum of the digits of a two-digit number is 9, and the tens digit is twice the units digit. Find this number.
b) The sum of the digits of a two-digit number is equal to the smallest two-digit number. The tens digit denotes a number 4 times smaller than the units digit. What is it two-digit number?
What incorrectness is allowed in the formulations of these tasks? Should they be corrected?
5. Each digit of a five-digit number is one more than the previous one, and the sum of its digits is 30. What is this number?
6. For younger students the task was proposed: "Write down 5 four-digit numbers using the numbers 2, 5, 0, 6 (the same digit should not be repeated in the number entry)". And how many all possible four-digit numbers can be written using the numbers 2, 5, 0 and 6 so that the same digit does not repeat in the number entry?
Addition algorithm
Single-digit addition can be performed based on the definition of this action, but in order not to refer to the definition every time, all the sums that are obtained by adding single-digit numbers are recorded in a special table called the single-digit addition table and memorized.
Naturally, the meaning of addition is also preserved for multi-digit numbers, but the practical implementation of addition occurs according to special rules. The sum of multi-digit numbers is usually found by performing column addition. For example,
Let us find out how this algorithm arises, what theoretical provisions underlie it.
We represent the terms 341 and 7238 as the sum of powers of ten with coefficients:
341 + 7238 = (3∙10 2 + 4∙10 + 1) + (7∙10 3 + 2∙10 2 + 3∙10 + 8). Let's open the brackets in the resulting expression, swap and group the terms so that the ones are next to the ones, tens to tens, etc. All of these transformations can be performed based on the corresponding addition properties. The associativity property allows you to write an expression without brackets: 3∙10 2 + 4∙10 + 1 + 7∙10 3 + 2∙10 2 + 3∙10 + 8.
Based on the commutativity property, we swap the terms: 7∙10 3 + 3∙10 2 + 2∙10 2 + 4∙10 + 3∙10 + 1+8. According to the associativity property, we will group: 7∙10 3 + (3∙10 2 + 2∙10 2) + (4∙10 + 3∙10) + (1 + 8). Let's take out the number 10 2 in the first selected group, and 10 in the second one. This can be done in accordance with the distributive property of multiplication with respect to addition: 7∙10 3 + 5∙10 2 + 7∙10 + 9.
So, the addition of these numbers 341 and 7238 was reduced to the addition of single-digit numbers, depicted by the numbers of the corresponding digits. These amounts are found in the addition table. The resulting expression is the decimal representation of the number 7579.
We see that the following theoretical facts underlie the multi-digit addition algorithm:
The way to write numbers in the decimal number system;
Properties of commutativity and associativity of addition;
Distributivity of multiplication with respect to addition;
Addition table for single digit numbers.
It is easy to see that in the case of adding numbers “with the transition through a dozen”, the theoretical foundations of the addition algorithm will be the same. Consider, for example, the sum 748 + 436.
We represent the terms as a sum of powers of ten with the corresponding coefficients: (7∙10 2 + 4∙10 + 8) + (4∙10 2 + 3∙10 + 6). Let's use the properties of addition and the distributivity of multiplication with respect to addition and transform the resulting expression into the following form: (7 + 4) ∙10 2 + (4 + 3) ∙10 + (8 + 6). We see that in this case the addition of these numbers also reduced to the addition of single-digit numbers, but the sums 7 + 4, 8 + 6 exceed 10 and therefore the last expression is not a decimal representation of the number. It is necessary to make sure that the coefficients in front of the powers of 10 are less than 10. To do this, we perform a number of transformations. First, we represent the sum 8 + 6 as 1∙10 + 4:
Then we will use the properties of addition and multiplication and bring it to the form: (7 + 4) ∙10 2 + (4 + 3 + 1) ∙10 + 4. The essence of the last transformation is as follows: ten, which was obtained by 1 addition of units, add to tens of given numbers. And finally, writing the sum 7 + 4 as 1∙10+ 1, we get: (1∙10 + 1)10 2 + 8∙10 + 4. The last expression is the decimal representation of the number 1184. Therefore. 748+436= 1184.
Let us derive an algorithm for adding multi-valued numbers in a general form. Let the numbers be given:
x= a n 10 n + a n -1 10 n -1 + ... + a 1 10 + a 0 ,
at= b n 10 n + b n -1 10 n -1 + ... + b 1 10 + b 0 ,
x + y = (a n + b n)10n+(a n-1 + b n-1) 10 n-1 + ... +(a 1 + b 1) 10+(a 0 + b 0)
The transformations are based on the properties of associativity and commutativity
addition, as well as the distributivity of multiplication with respect to addition.
Only if all the sums ak + bk do not exceed 9, the addition operation can be
consider completed. Otherwise, choose the smallest To, for which a to+ b to> 10. If a to+ b to> 10, then from the fact that 0<a to<
9 and 0< b to<
9, the inequality 0< a to+ b to<
18 and so a to+ b to can also be represented as a to+ b to= 10 + with k, where 0< from to<
9. But then (and to+ b k) 10 k =(10 + with k) · 10To = 10 To +1 + from to · 10 etc.
In the case when the decimal entries of the terms have a different number of digits, it is necessary to attribute to the number with a smaller number of digits, several zeros in front, equalizing the number of digits in both terms. After that, the addition process described above is applied.
In general terms, the algorithm for adding natural numbers written in the decimal number system is formulated as follows:
1. Write the second term under the first so that the corresponding digits are one under the other.
2. Add up the units of the first digit. If the sum is less than ten, write it down in the units of the answer and move on to the next digit (tens).
3. If the sum of units is greater than or equal to ten, then represent it in the form a o + b o ~ 1 10 + with 0 , Where from 0 - single digit; write down With () into the category of units of the answer and add 1 to the tens of the first term, after which they go to the category of tens.
4. Repeat the same actions with tens, then with hundreds, etc. The process ends when the digits of the most significant digits are added. In this case, if their sum is greater than or equal to ten, then we assign zeros in front of both terms, increase zero in front of the first term by 1 and perform the addition 1+0=1.
Note that in this algorithm (as in some others), for brevity, the term "digit" is used instead of "a single-digit number represented by a digit."
Exercises
1. Using the example of adding numbers 237 and 526, show what theoretical facts underlie the algorithm for adding multi-valued numbers.
2. When studying the algorithm for adding three-digit numbers in elementary school, the following cases of addition are consistently considered:
231 + 342; 425 + 135; 237 + 526; 529 + 299. What are the characteristics of each of these cases?
3. Calculate orally the value of the expression; justify the method used:
a) 2746 + 7254 + 9876; b) 7238 + 8978 + 2768;
c) (4729 + 8473) + 5271; d) 4232 + 7419 + 5768 + 2591;
e) (357 + 768 + 589) + (332 + 211 + 643).
4. What reasoning of schoolchildren will you consider correct when completing the assignment.
a) Is it possible to assert that the values of the sums in each column are the same:
2459+ 121 53075 + 2306
2458+ 122 53076 + 2305
2457+123 53006 + 2375
2456+ 124 53306 + 2075
b) Is it possible to write the values of these sums in ascending order:
4583 + 321 4593 + 311 4573 + 331
