At school they study the multiplication table, and then teach children to multiply numbers in a column. Of course, this is not the only way to multiply. In fact, there were several dozen ways to multiply and divide multi-digit numbers. I will give here, perhaps, an even simpler “lattice method” (see the book by I.Ya. Depman, N.Ya. Vilenkin “Beyond the Pages of a Textbook”). Let's look at this method with an example.
Let's say we need to multiply 347 by 29. Let's draw a table, as in Figure a), write above it the number 347 from left to right, and to the right of it - the number 29 from top to bottom. In each cell we write the product of the numbers above this cell and to the right of it. In this case, we will write the tens digit of the product above the slash, and the units digit below it. Now we will add the numbers in each oblique stripe shown in the figure, performing this operation from right to left. If the amount is less than 10, then it is written under the bottom number of the strip. If it turns out to be more than 10, then only the units digit of the amount is written, and the tens digit is added to the next amount. As a result, we obtain the desired product, which is equal to 10063.

This method of multiplication was previously common in the East and Italy. To understand its meaning, let's look at figure b). We see that in the first stripe there are units, in the second – tens, in the third – hundreds, etc. In other words, the product 347\cdot29 is calculated as follows:
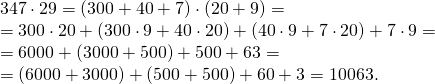
There are some other rules to help quick counting. So, to square two-digit number ending in 5, you need to add 1 to the first digit and multiply the resulting number by this digit, and then add 25 to the result. For example, let's square 35. The first digit of this number is 3, add 1: 3+1=4. Let's multiply 3 by 4, we get 12, then we just add 25. So the answer is: 1225.
This rule follows immediately from the fact that
Of course, this can also be used to square three-digit numbers ending in 5 and numbers that have even more digits. However, in these cases, you will have to calculate the product a\cdot(a+1) , where the number a already has several decimal places, and this also has to be done, say, in a column, that is, this is more complicated!
And now the video shows a method of multiplication, widely viewed and discussed on the Internet, which is called the Chinese method. Funny and interesting. By the way, some generalizations of this method have already been posted, because drawing 9 straight lines when multiplying by 9 is somehow long and uninteresting, and then counting the intersection points... In general, you still need to know the multiplication table! I think you can explain why the method works. Attention, question: why?
In essence, the whole difficulty lies in how to correctly place the intermediate results of multiplication (partial products). In an effort to simplify calculations, people have come up with many ways to multiply numbers. Over the centuries-old history of mathematics, there have been several dozen of them.
The heritage of the Hindus is the lattice method.
The Hindus, who knew the decimal number system from ancient times, preferred oral counting to written counting. They invented several ways fast multiplication. Later they were borrowed by the Arabs, and from them these methods were passed on to the Europeans. Those, however, did not limit themselves to them and developed new ones, in particular the one that is studied at school - multiplication by column. This method has been known since the beginning of the 15th century; in the next century it firmly came into use among mathematicians, and today it is used everywhere. But is multiplication a column? the best way performing this arithmetic operation? In fact, there are other, now forgotten, methods of multiplication that are no worse, for example, the lattice method.
This method was used in ancient times, in the Middle Ages it became widespread in the East, and in the Renaissance - in Europe. The grid method was also called Indian, Muslim or “Cellular Multiplication”. And in Italy it was called “Gelosia”, or “lattice multiplication” (Gelosia translated from Italian means “blinds”, “lattice shutters”. Indeed, the resulting figures from numbers were similar to shutters - blinds that covered windows from the sun Venetian houses.
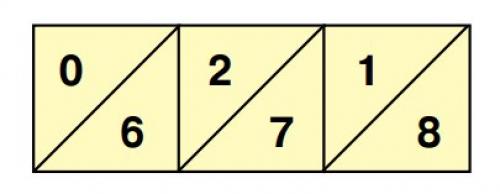
We will explain the essence of this simple method of multiplication with an example: we will calculate the product 296 x 73. Let's start by drawing a table with square cells, in which there will be three columns and two rows, according to the number of digits in the factors. Divide the cells in half diagonally. Above the table we write the number 296, and on the right side vertically - the number 73. Multiply each digit of the first number with each digit of the second and write the products in the corresponding cells, placing the tens above the diagonal and the ones below it. We obtain the digits of the desired product by adding the digits in the oblique stripes. In this case, we will move clockwise, starting from the lower right cell: 8, 2 1 7, etc. We will write the results under the table, as well as to the left of it. In the event that the addition results in a two-digit sum, we indicate only the ones, and add the tens to the sum of the digits from the next strip. Answer: 21,608. So, 296 x 73 = 21,608.
The lattice method is in no way inferior to column multiplication. It is even simpler and more reliable, despite the fact that the number of actions performed in both cases is the same. Firstly, you only have to work with single and double digit numbers, and they are easy to operate with in your head. Secondly, there is no need to remember intermediate results and keep track of the order in which they are written down. Memory is unloaded and attention is retained, so the likelihood of error is reduced. In addition, the lattice method allows you to get results faster. Once you master it, you can see for yourself.
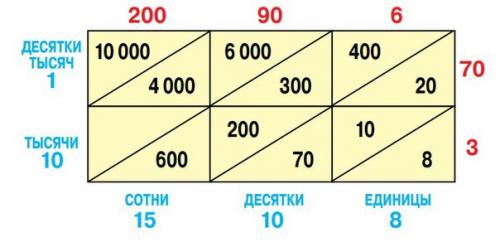
Why does the lattice method lead to the correct answer? What is its “Mechanism”? Let's figure this out using a table constructed similarly to the first one, only in this case the factors are presented as the sums of 200 90 6 and 70 3.

As you can see, in the first oblique stripe there are units, in the second - tens, in the third - hundreds, etc. when added, they give the answer, respectively, the number of units, tens, hundreds, etc. the rest is obvious:
10 10 1500. 100. 8 _ 21608.
In other words, in accordance with the laws of arithmetic, the product of the numbers 296 and 73 is calculated as follows:
296 x 73 = (200 90 6) x (70 3) = 14,000 6300 420 600 270 18 = 10,000 (4000 6000) (300 400 600 200) (70 20 10) 8 = 21,608.
Nepera sticks.
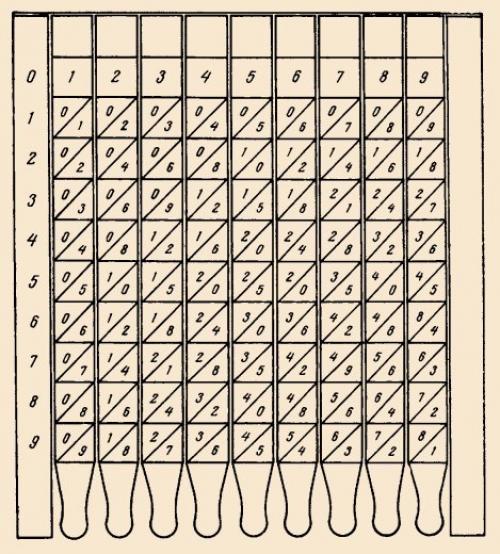
Multiplication using the lattice method is the basis of a simple and original calculating device - neper sticks.
Its inventor, John Napier, a Scottish baron and a lover of mathematics, worked with professionals to improve the means and methods of calculation. In the history of science, he is known primarily as one of the creators of logarithms.
The device consists of ten rulers on which the multiplication table is placed. In each cell, divided by a diagonal, the product of two single-digit numbers from 1 to 9 is written: the number of tens is indicated in the upper part, the number of units is indicated in the lower part. One ruler (the left one) is stationary, the rest can be rearranged from place to place, laying out the desired number combination. Using neper sticks, it is easy to multiply multi-digit numbers, reducing this operation to addition.
For example, to calculate the product of the numbers 296 and 73, you need to multiply 296 by 3 and 70 (first by 7, then by 10) and add the resulting numbers. Let's attach three others to the fixed ruler - with the numbers 2, 9 and 6 at the top (they should form the number 296. Now let's look at the third line (the line numbers are indicated on the outer ruler. The numbers in it form a set that is already familiar to us.
Adding them, as in the lattice method, we get 296 x 3 = 888. Likewise, ra? 6
The combinatory property of multiplication indicates to us the equality of two products a·(b·c) and (a·b)·c, where a, b And c– any natural numbers. Thus, the result of multiplying three numbers a, b And c does not depend on the way the brackets are placed. Because of this, in the products a·(b·c) and (a·b)·c, parentheses are often not placed, and the products are written in the form a·b·c. Expression a·b·c called the product of three numbers a, b And c, numbers a, b And c all are also called multipliers.
Similarly, the associative property of multiplication allows us to state that the products (a b) (c d) , (a (b c)) d , ((a b) c) d , a (b ·(c·d)) and a·((b·c)·d) are equal. That is, the result of multiplying four numbers also does not depend on the distribution of brackets. Product of four numbers a, b, c And d write it down as a b c d.
In general, the result of multiplying two, three, four, and so on numbers does not depend on the method of placing parentheses, and in writing such products, parentheses are usually omitted.
Now let's figure out how to calculate the product of several numbers, the notation of which does not contain parentheses. In this case multiplying three or more numbers is reduced to sequentially replacing two adjacent factors with their product until we get the required result. In other words, in writing the product, we place the brackets ourselves in any acceptable way, after which we sequentially multiply the two numbers.
Consider an example of calculating the product of five natural numbers 2 , 1 , 3 , 1 And 8 . Let's write down the product: 2 1 3 1 8. We will show two methods of solution (there are more than two methods of solution).
First way. We will successively replace the two factors on the left with their product. Since the result of multiplying numbers 2 And 1 is the number 2 , That 2·1·3·1·8=2·3·1·8. Because 2·3=6, That 2·3·1·8=6·1·8. Further, because 6·1=6, That 6·1·8=6·8. Finally, 6·8=48. So, the product of five numbers 2 , 1 , 3 , 1 And 8 equals 48 . This solution corresponds to the following method of arranging brackets: (((2 1) 3) 1) 8.
Second way. Let's arrange the brackets in the product like this: ((2 1) 3) (1 8) . Because 2 1=2 And 1·8=8, then ((2·1)·3)·(1·8)=(2·3)·8 . Two times three is six, then (2·3)·8=6·8. Finally, 6·8=48. So, 2·1·3·1·8=48.
Note that the result of multiplying three or more numbers is not affected by the order of the factors. In other words, the factors in the product can be written in any order, and can also be swapped. This statement follows from the properties of multiplication of natural numbers.
Let's look at an example.
Multiply four numbers 3 , 9 , 2 And 1 . Let's write down their product: 3·9·2·1. If we replace the factors 3 And 9 their product or factors 9 And 2 their product, then at the next stage we will have to multiply by two-digit numbers 27 or 18 (which we don’t know how to do yet). You can do without this by swapping the terms and arranging the brackets in a certain way. We have 3·9·2·1=3·2·9·1=(3·2)·(9·1)=6·9=54.
Thus, by swapping the factors, we can calculate the products in the most convenient way.
To complete the picture, consider a problem whose solution boils down to multiplying several numbers.
Example.
Each box contains 3 subject. Each box contains 2 boxes. How many items are contained in 4 boxes?
Solution.
Since in one box there are 2 boxes, each of which 3 item, then in one box there is 3·2=6 items. Then in four drawers there is 6·4=24 subject.
One can argue differently. Since in one box there are 2 boxes, then in four boxes there are 2·4=8 boxes Since each box contains 3 subject, then in 8 boxes are 3·8=24 subject.
The announced solutions can be briefly written as (3·2)·4=6·4=24 or 3·(2·4)=3·8=24.
Thus, the required number of objects is equal to the product of the numbers 3 , 2 And 4 , that is, 3·2·4=24.
Answer:
Let's summarize the information in this paragraph.
Multiplying three or more natural numbers is a sequential multiplication of two numbers. In addition, due to the commutative and combinative properties of multiplication, the factors can be swapped and any two of the multiplied numbers can be replaced with their product.
Multiplying a sum by a natural number and a natural number by a sum.
Addition and multiplication of numbers are related by the distributive property of multiplication. This property allows you to study addition and multiplication together, which opens up much more opportunities than studying these actions separately.
We formulated the distribution property of multiplication relative to addition for two terms: (a+b) c=a c+b c , a, b, c– arbitrary natural numbers. Starting from this equality, we can prove the validity of the equalities (a+b+c) d=a d+b d+c d , (a+b+c+d) h=a h+b h+c h+d h etc., a, b, c, d, h– some natural numbers.
Thus, the product of the sum of several numbers and a given number is equal to the sum of the products of each of the terms and the given number. This rule can be used when multiplying a sum by a given number.
For example, let's multiply the sum of five numbers 7 , 2 , 3 , 8 , 8 per number 3 . Let's use the resulting rule: (7+2+3+8+8) 3=7 3+2 3+3 3+8 3+8 3. Because 7·3=21, 2·3=6, 3·3=9, 8·3=24, That 7·3+2·3+3·3+8·3+8·3=21+6+9+24+24. It remains to calculate the sum of five numbers 21+6+9+24+24=84 .
Of course, it was possible to first calculate the sum of the five given numbers, and then carry out the multiplication. But in this case we would have to multiply a two-digit number 7+2+3+8+8=28 per number 3 , which we don’t know how to do yet (we’ll talk about multiplying such numbers later in the section).
The commutative property of multiplication allows us to reformulate the rule for multiplying the sum of numbers by a given number as follows: the product of a given number and the sum of several numbers is equal to the sum of the products of a given number and each of the terms. This is the rule for multiplying a given number by a sum.
Here is an example of using the rule for multiplying a number by a sum: 2·(6+1+3)=2·6+2·1+2·3=12+2+6=20.
Let's look at a problem whose solution boils down to multiplying the sum of numbers by a given number.
Example.
Each box contains 3 red, 7 green and 2 blue items. How many items are in the four boxes?
Solution.
One box contains 3+7+2 items. Then there are (3+7+2)·4 items in four boxes. Let's calculate the product of the sum and the number using the resulting rule: (3+7+2) 4=3 4+7 4+2 4=12+28+8=48.
Answer:
48 items.
Multiplying a natural number by 10 , 100 , 1 000 and so on.
First, let's get the rule for multiplying an arbitrary natural number by 10 .
Natural numbers 20
, 30
, …, 90
inherently correspond 2
dozens, 3
dozens... 9
dozens, that is, 20=10+10
, 30=10+10+10
, ... Since we gave the multiplication of two natural numbers the meaning of the sum of identical terms, we have
2·10=20, 3·10=30, ..., 9·10=90.
Reasoning similarly, we arrive at the following equalities:
2·100=200, 3·100=300, ..., 9·100=900;
2·1 000=2 000, 3·1 000=3 000, ..., 9·1 000=9 000;
2·10,000=20,000, 3·10,000=30,000, ..., 9·10,000=90,000; ...
Since ten tens is a hundred, then 10·10=100;
since ten hundreds is a thousand, then 100·10=1,000;
since ten thousand is ten thousand, then 1,000·10=10,000.
Continuing these arguments, we have 10,000·10=100,000, 100,000·10=1,000,000, …
Let's now look at an example that will allow us to formulate a rule for multiplying an arbitrary natural number by ten.
Example.
Multiply a natural number 7 032 on 10 .
Solution.
For this number 7 032 Let us present it as a sum of digit terms, after which we will use the rule for multiplying the sum by the number that we obtained in the previous paragraph of this article: 7,032·10=(7,000+30+2)·10= 7,000·10+30·10+ 2·10.
Because 7 000=7 1 000 And 30=3·10, then the resulting amount 7 000 10+30 10+2 10 equal to the sum (7 1 000) 10+(3 10) 10+2 10, and the associative property of multiplication allows us to write the following equality:
(7 1 000) 10+(3 10) 10+2 10= 7·(1,000·10)+3·(10·10)+2·10.
By virtue of the results written before this example, we have 7·(1,000·10)+3·(10·10)+2·10= 7·10,000+3·100+2·10= 70,000+300+20.
Amount received 70 000+300+20 represents the expansion into digits of a number 70 320 .
Answer:
7,032·10=70,320.
By performing similar actions, we can multiply any natural number by ten. At the same time, it is not difficult to notice that as a result we will receive numbers, the writing of which will differ from the writing of the number being multiplied only by a digit 0 , located on the right.
All the above considerations allow us to voice rule for multiplying an arbitrary natural number by ten: if in the notation of a given natural number, add a digit to the right 0 , then the resulting entry will correspond to the number that is the result of multiplying this natural number by 10 .
For example, 4·10=40, 43·10=430, 501·10=5 010, 79,020·10=790,200 etc.
And now, based on the rule of multiplying a natural number by 10 , we can get the rules for multiplying an arbitrary natural number by 100 , on 1 000 etc.
Because 100=10·10, then multiplying any natural number by 100
comes down to multiplying this number by 10
10
. For example,
17·100=17·10·10=170·10=1,700;
504·100=504·10·10=5,040·10=50,400;
100 497 100=100 497 10 10= 1 004 970 10=10 049 700.
That is, if you add two digits to the right of the number being multiplied 0 , then we get the result of multiplying this number by 100 . This is it rule for multiplying a natural number by 100 .
Because 1 000=100·10, then multiplying any natural number by a thousand is reduced to multiplying this number by 100 and then multiplying the result by 10 . From these reasoning it follows rule for multiplying an arbitrary natural number by 1 000 : if you add three digits to the right of a number 0 , then we get the result of multiplying this number by a thousand.
Similarly, when multiplying a natural number by 10 000 , 100 000 and so on, you need to add four numbers to the right, respectively 0 , five digits 0 and so on.
For example,
58·1 000=58 000;
6,032·1,000,000=6,032,000,000;
777·10 000=7 770 000.
Multiplication of multi-valued and single-valued natural numbers.
Now we have all the skills necessary to perform multi-digit and single-digit multiplication of natural numbers.
What needs to be done for this?
Let's immediately understand it with an example.
Example.
Let's multiply three digit number 763 to a single digit number 5 , that is, we calculate the product 763·5.
Solution.
First you need to imagine multi-digit number in the form of a sum of bit terms. In our example 763=700+60+3 , then we have 763·5=(700+60+3)·5.
Now we apply: (700+60+3) 5=700 5+60 5+3 5.
Because 700=7·100 And 60=6·10(we talked about this in the previous paragraph), then the amount 700·5+60·5+3·5 can be written as (7 100) 5+(6 10) 5+3 5.
Due to the commutative and combinative properties of multiplication, the following equality is true: (7 100) 5+(6 10) 5+3 5= (5 7) 100+(5 6) 10+3 5 .
Because 5·7=35, 5·6=30 And 3·5=15, then (5·7)·100+(5·6)·10+3·5= 35·100+30·10+15.
All that remains is to multiply by 100
and on 10
, then add the three terms:
35 100+30 10+15=
3 500+300+15=3 815
Answer:
Work 763 And 5 equals 3 815 .
It is clear that multiplication single digit number for a multi-digit number is carried out in a similar way.
To consolidate the material, we will give the solution to another example, but this time we will do without explanations.
Example.
3 And 104 558 .
Solution.
3 104 558= 3·(100,000+4,000+500+50+8)=
=3·100,000+3·4,000+ 3·500+3·50+3·8=
=3·100,000+3·(4·1,000)+ 3·(5·100)+3·(5·10)+3·8=
=3·100,000+(3·4)·1,000+ (3·5)·100+(3·5)·10+3·8=
=3·100,000+12·1,000+ 15 100+15 10+3 8=
=300 000+12 000+
1 500+150+24=313 674
Answer:
The result of multiplying numbers 3 And 104 558 is the number 313 674 .
Multiplying two multi-digit natural numbers.
Now we have come to the culmination - the multiplication of two multi-digit natural numbers. The first thing you need to do is expand one of the factors into digits (usually the number whose entry consists of more signs), then use the rule for multiplying a number by a sum (or a sum by a number). Further calculations will not cause difficulties if you have mastered the information well previous sections this article.
Let's look at all the stages of multiplying two multi-digit natural numbers using an example.
Example.
Calculate product of numbers 41 And 3 806 .
Solution.
Natural number expansion 3 806 by digits has the form 3 000+800+6 , therefore, 41·3 806=41·(3 000+800+6) .
Let's apply the rule for multiplying a number by a sum: 41·(3,000+800+6)= 41·3,000+41·800+41·6.
Because 3,000=3·1,000 And 800=8·100, then the equality 41·3 000+41·800+41·6= is true 41·(3·1 000)+41·(8·100)+41·6.
The combinational property of multiplication allows us to rewrite the last sum in the following form (41·3)·1,000+(41·8)·100+41·6.
What is multiplication?
Multiplication is an arithmetic operation in which the first number is repeated as a term as many times as the second number shows.
A number that repeats as a term is called multiplyable(it is multiplied), the number that shows how many times to repeat the term is called multiplier. The number resulting from multiplication is called work.
For example, multiplying the natural number 2 by the natural number 5 means finding the sum of five terms, each of which is equal to 2:
2 + 2 + 2 + 2 + 2 = 10
In this example, we find the sum by ordinary addition. But when the number of equal terms is large, finding the sum by adding all the terms becomes too tedious.
Multiplication is indicated by the sign × (slash) or the sign · (dot) and reads: multiply by. The multiplication sign is placed between the multiplicand and the multiplier. The multiplicand is written to the left of the multiplication sign, and the multiplier is written to the right:
This entry reads like this: the product of 2 and 5 equals 10 or 2 times 5 equals 10.
Thus, we see that multiplication is simply a short form of adding like terms.
Multiplication check
To check multiplication, you can divide the product by the factor. If the result of division is a number equal to the multiplicand, then the multiplication is done correctly:
Now let's check the multiplication:
Multiplication can also be checked by dividing the product by the multiplicand. If the result of division is a number equal to the multiplier, then the multiplication is done correctly:
Let's check:
Multiplying one and by one
a the following equalities are true:
1 · a = a
a· 1 = a
- If the multiplicand is the number 1, then the product is equal to the multiplier. For example, 1 · 3 = 3 because the sum of 1 + 1 + 1 is three.
- If the factor is one, then the product will be equal to the multiplicand. For example, 5 · 1 = 5. If we take the number 5 once, we get 5.
Number 0 in multiplication
For any natural number a the following equalities are true:
a· 0 = 0
0 · a = 0
These equalities mean the following:
- If the factor is zero, then the product is zero. For example, 5 · 0 = 0 (if we don’t take 5 even once, then naturally we won’t get anything).
- If the multiplicand is zero, then the product is zero. For example, 0 · 3 = 0 because the sum of 0 + 0 + 0 is zero.



