This article provides a detailed overview dividing numbers with different signs . First, the rule for dividing numbers with different signs is given. Below are examples of dividing positive numbers by negative and negative numbers to positive.
Page navigation.
Rule for dividing numbers with different signs
In the article division of integers, a rule for dividing integers with different signs was obtained. It can be extended to both rational numbers and real numbers by repeating all the reasoning from the above article.
The rules that govern multiplication and division of numbers are very similar. The key is to identify whether the signs of the given two numbers are the same or different because this will determine the final sign of the answer. Example 1. Find the product and coefficient 12 ÷ 6.
Since the numbers 3 and 6 have the same signs, their product is positive. Since the numbers 12 and 6 have the same signs, their coefficient is positive. Example 2. Find the product and factor -21 ÷. The numbers -5 and -3 both have negative signs. The presence of identical signs means that their product must also be positive.
So, rule for dividing numbers with different signs has the following wording: to divide positive number for a negative number or a negative number for a positive one, you must divide the dividend by the modulus of the divisor, and put a minus sign in front of the resulting number.
Let's write this division rule using letters. If the numbers a and b have different signs, then the formula is valid a:b=−|a|:|b| .
Find the quotient -21 ÷. . The factor of two numbers with the same signs is positive. Example 3: Multiply numbers and divide numbers 18 ÷. The number 9 has a positive sign, and the number -3 has negative sign. Multiplying these two numbers with different signs should give a negative answer.
The number 9 is positive and -3 is negative. Dividing two numbers with different signs should give a negative answer. Example 4: Simplify the numerical expression. We can do this to simplify the numerator by multiplying two numbers. Do the same with the denominator.
Rule for multiplying numbers with different signs
The numbers in the numerator have different signs, so we expect their product to be negative. Meanwhile, the denominator has numbers with the same signs, so their product must be positive. We'll finish this by dividing the numerator by the denominator. Remember also the rule of separation. The numerator is negative and the denominator is positive, having different signs, must give a negative answer.
From the stated rule it is clear that the result of dividing numbers with different signs is a negative number. Indeed, since the modulus of the dividend and the modulus of the divisor are positive numbers, their quotient is a positive number, and the minus sign makes this number negative.
Note that the rule considered reduces the division of numbers with different signs to the division of positive numbers.
Example 5: Multiply numbers. So far we have been multiplying numbers two at a time. This time we have a situation where we are looking for a product of three or more numbers. We can do this by multiplying two numbers at a time because we know how to do it. But there is quick way determine the sign without having to multiply them two at a time.
Note that we have an even number of negative signs, i.e. four negative numbers. If you encounter something like this, use the rule. An even number of negative signs means we expect the answer to be positive. Example 6: Multiply numbers.
You can give another formulation of the rule for dividing numbers with different signs: to divide the number a by the number b, you need to multiply the number a by the number b −1, the inverse of the number b. That is, a:b=a b −1 .
This rule can be used when it is possible to go beyond the set of integers (since not every integer has an inverse). In other words, it applies to the set of rational numbers as well as the set of real numbers.
Rule for dividing numbers with different signs
This problem is not intended to trick you. Instead, think of this as another opportunity to learn how to approach the question this way. Your teacher might throw something similar to this on your quiz to see how well you know the topic.
Examples of dividing numbers with different signs
Regardless of the signs, all numbers are the same. Therefore, we predict that the answer can be either 1 or -1. Counting the number of negative signs, we have nine, which is strange! An odd number of negative signs means our final answer must be negative.
It is clear that this rule for dividing numbers with different signs allows you to move from division to multiplication.
The same rule is used when dividing negative numbers.
It remains to consider how this rule for dividing numbers with different signs is applied when solving examples.
Examples of dividing numbers with different signs
Let us consider solutions to several characteristic examples of dividing numbers with different signs to understand the principle of applying the rules from the previous paragraph.
Example 7: Divide the numbers ÷ ÷ ÷ ÷ ÷ ÷ ÷. The rule for odd and even numbers of negative numbers also works when dividing numbers. Since we have a count of seven negative digits, an odd number, the answer must be negative. ÷ ÷ ÷ ÷ ÷ ÷ = - 1.
Multiplication is one of the basic forms of mathematics. Below we explain how to multiply numbers together, what the commutative law is, and what you really need in total. In addition, there are examples and exercises with solutions for teaching multiplication. Multiplication allows you to solve many mathematical problems, even if it doesn't seem like it at first glance. For example, you can simply calculate areas, volumes or interest rates. But before we get to that, we need to learn the basics.
Example.
Divide the negative number −35 by the positive number 7.
Solution.
The rule for dividing numbers with different signs prescribes first finding the modules of the dividend and divisor. The modulus of −35 is 35, and the modulus of 7 is 7. Now we need to divide the module of the dividend by the module of the divisor, that is, we need to divide 35 by 7. Remembering how division of natural numbers is performed, we get 35:7=5. The last step left in the rule for dividing numbers with different signs is to put a minus in front of the resulting number, we have −5.
This is multiplication, you can see between two numbers. For example, it looks like this: 5 This symbol is therefore a multiplication sign. The number before the symbol is also called the factor 1 or multiplier. The second number is called the factor of 2 or the multiplier. The result of multiplication is a product. The following review illustrates this again.
Note: Multiplication is a short form of addition, as the following examples show. Let's now move on to calculating products using some examples. Look at these times and then there are some explanations. Let's look at the first example: the number 5 is written 3 times and then added. In the second example it's the opposite. The number 3 is written five times and added. The same principle applies to the other two examples. Note. If you have a multiplication exercise, you no longer write down the sums, but you know that 4 4 = 16.
Here's the whole solution: .
It was possible to proceed from a different formulation of the rule for dividing numbers with different signs. In this case, we first find the inverse of the divisor 7. This number is the common fraction 1/7. Thus, . It remains to multiply numbers with different signs: . Obviously, we came to the same result.
For anyone, however, who is relearning multiplication, summing up makes perfect sense. In any case, complete the exercises at the end of this chapter. The special position in multiplication is multiplied by a number, the result is always zero. Several examples illustrate this.
The so-called commutative law applies to multiplication. But it's not complicated: this law of mathematics simply says that 3 5 has exactly the same result as 5 3 = If you don't believe this, just try it yourself or look at the following examples. Multiplying and dividing negative numbers. Multiplication: Called the reduction of adding equal amounts. Division: Some believe that this operation is selfish because it involves division. On the contrary, it is a clear expression of justice. She is responsible for sharing and always does so in equal parts.
Answer:
(−35):7=−5 .
Example.
Calculate the quotient 8:(−60) .
Solution.
According to the rule for dividing numbers with different signs, we have 8:(−60)=−(|8|:|−60|)=−(8:60)
. The resulting expression corresponds to a negative ordinary fraction (see the division sign as a fraction bar), you can reduce the fraction by 4, we get 
.
Properties of Multiplication
Its elements are: dividend, divisor and coefficient. Multiplication of integers also has properties similar to those of natural numbers. It states that multiplying a sum by a number gives the same result as multiplying each by adding the number and then adding all the products. Neutral element.
- Commuting property.
- Distribution property.
Multiplying integers such as a sum requires that the sign and absolute value of the result be determined separately. When multiplying two integers, the absolute value and sign of the result are determined as follows. The absolute value is the product of the absolute values of the factors.
Let's write down the whole solution briefly: .
Answer:
.
When dividing fractional rational numbers with different signs, their dividend and divisor are usually represented as ordinary fractions. This is due to the fact that it is not always convenient to perform division with numbers in other notation (for example, in decimal).
Sign, if the signs of the factors are equal, and if they are different. To remember the sign of the result, the sign rule is also used. × = More for more than more. × = More with less than less. × = Less for more equal less. × = Less than less.
The product of absolute values is 4 × 6 =. The sign of the factors is identical, so the sign of the result is identical. The product of absolute values is 5 × 3 =. The product of absolute values is 7 × 8 =. The sign of the factors is the same, so the sign of the result is equal. The product of absolute values is 9 × 2 =.
Example.
Solution.
The module of the dividend is equal to , and the module of the divisor is equal to 0,(23) . To divide the modulus of the dividend by the modulus of the divisor, let's move on to ordinary fractions.
Let's convert a mixed number to an ordinary fraction: 
, and also convert the periodic decimal fraction into an ordinary fraction: .
The rules that were derived for multiplication work just fine when dividing rational numbers. Dividing equal signs gives a positive sign, while dividing different signs gives a negative sign. When dividing fractions, changing the place of the divisor and dividend, the result of the division changes, but not the sign.
In the Integers course, you explained what integers are, how they are ordered, as well. The peculiarity of the need to multiply and divide integers in relation to multiplications and divisions is that we now multiply and divide also the sign of each integer.
Thus, .
In this article we will deal with multiplying numbers with different signs. Here we will first formulate the rule for multiplying positive and negative numbers, justify it, and then consider the application of this rule when solving examples.
If you got here, it's probably because you can't solve some exercise. You just have to allow yourself to be guided by me, you will see how your note and your free time will rise like foam. We use the sign rule to find out the result of multiplication and division of the sign of integers.
More between more than more More between less less Less less less Less between more less.
- Equal signs, greater result.
- When multiplying or dividing different signs, the result is less.
Page navigation.
Rule for multiplying numbers with different signs
Multiplying a positive number by a negative number, as well as a negative number by a positive number, is carried out as follows: the rule for multiplying numbers with different signs: to multiply numbers with different signs, you need to multiply and put a minus sign in front of the resulting product.
Multiply the numbers: 3 = 15. And all the numbers will be multiplied. We will multiply these other multiplications in the same way. And open the keys that will let you. Learn to solve your problems and exercises. Keep moving towards the ledge. Be more effective in learning math.
Check your inbox or spam to confirm your subscription
Your data is protected and you can unsubscribe at any time. You will also receive others useful tips and random surprises from time to time. To divide integers, we will follow the following steps.
- The sign is divided taking into account the rule of signs.
- Numbers are divided.
Let's write this rule down in letter form. For any positive real number a and any negative real number −b, the equality a·(−b)=−(|a|·|b|) , and also for a negative number −a and a positive number b the equality (−a)·b=−(|a|·|b|) .
The rule for multiplying numbers with different signs is fully consistent with properties of operations with real numbers. Indeed, on their basis it is easy to show that for real and positive numbers a and b a chain of equalities of the form a·(−b)+a·b=a·((−b)+b)=a·0=0, which proves that a·(−b) and a·b are opposite numbers, which implies the equality a·(−b)=−(a·b) . And from it follows the validity of the multiplication rule in question.
We divide signs: more between less and less. And we already have our division of integers. Here are more examples, with other sign combinations you might find. You may find that the minus sign is in front of the fraction. In this case, the minus sign may not be clear in the numerator or denominator, since it does not change the result.
Integer operations with parentheses
When we have integer operations with parentheses, we have a special case of integer multiplication. The minus sign in front of the parenthesis is equivalent to multiplying each number of the parentheses by -1, so it changes the sign of the numbers inside. We have removed the parentheses according to. We multiply the minus sign by each sign of each number. 2 is positive because it carries nothing.
It should be noted that the stated rule for multiplying numbers with different signs is valid both for real numbers and for rational numbers and for integers. This follows from the fact that operations with rational and integer numbers have the same properties that were used in the proof above.
Do you need help with math?
We can also add and subtract first in parentheses and then multiply the result by the minus sign, as in this example. Likewise, the sign in front of the parenthesis is equivalent to multiplying by 1 and leaves the numbers inside the parenthesis with the same sign. All with simple and pleasant language that you will understand perfectly. You will know the exact steps you should give to solve your exercises and problems. You will get results in a very short time without spending more time trying to figure it out on your own without achieving any result. Why does it take 2 hours on the Internet when you can find out in less than 20 minutes?
It is clear that multiplying numbers with different signs according to the resulting rule comes down to multiplying positive numbers.
It remains only to consider examples of the application of the disassembled multiplication rule when multiplying numbers with different signs.
Examples of multiplying numbers with different signs
Let's look at several solutions examples of multiplying numbers with different signs. Let's start with a simple case to focus on the steps of the rule rather than the computational complexity.
Example.
Multiply the negative number −4 by the positive number 5.
Solution.
According to the rule for multiplying numbers with different signs, we first need to multiply the absolute values of the original factors. The modulus of −4 is 4, and the modulus of 5 is 5, and multiplying the natural numbers 4 and 5 gives 20. Finally, it remains to put a minus sign in front of the resulting number, we have −20. This completes the multiplication.
Briefly, the solution can be written as follows: (−4)·5=−(4·5)=−20.
Answer:
(−4)·5=−20.
When multiplying fractions with different signs, you need to be able to multiply ordinary fractions, multiply decimals and their combinations with natural and mixed numbers.
Example.
Multiply numbers with different signs 0, (2) and .
Solution.
By converting a periodic decimal fraction into a common fraction, and also by converting from a mixed number to an improper fraction, from the original product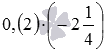 
we will come to the product of ordinary fractions with different signs of the form . This product, according to the rule of multiplying numbers with different signs, is equal to . All that remains is to multiply common fractions in parentheses, we have 
.
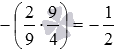Answer:
.
Separately, it is worth mentioning the multiplication of numbers with different signs, when one or both factors are
