The focus of this article is division negative numbers . First, the rule for dividing a negative number by a negative is given, its justification is given, and after that examples of dividing negative numbers with detailed description decisions.
Page navigation.
Rule for dividing negative numbers
Before giving the rule for dividing negative numbers, let us recall the meaning of the operation of division. Division at its core represents finding an unknown factor from a known product and a known other factor. That is, the number c is the quotient of a divided by b when c·b=a, and vice versa, if c·b=a, then a:b=c.
Rule for dividing negative numbers the following: the quotient of dividing one negative number by another is equal to the quotient of dividing the numerator by the modulus of the denominator.
Let's write down the sounded rule using letters. If a and b are negative numbers, then the equality is true a:b=|a|:|b| .
The equality a:b=a b −1 is easy to prove, starting from properties of multiplication of real numbers and definitions of reciprocal numbers. Indeed, on this basis we can write a chain of equalities of the form (a b −1) b=a (b −1 b)=a 1=a, which, due to the meaning of division mentioned at the beginning of the article, proves that a·b −1 is the quotient of a divided by b.
And this rule allows you to move from dividing negative numbers to multiplying.
It remains to consider the application of the considered rules for dividing negative numbers when solving examples.
Examples of dividing negative numbers
Let's sort it out examples of dividing negative numbers. Let's start with simple cases on which we will work out the application of the division rule.
Example.
Divide negative −18 by negative −3, then calculate the quotient (−5):(−2) .
Solution.
According to the rule for dividing negative numbers, the quotient of dividing −18 by −3 is equal to the quotient of dividing the absolute values of these numbers. Since |−18|=18 and |−3|=3, then (−18):(−3)=|−18|:|−3|=18:3 , all that remains is to divide the natural numbers, we have 18:3=6.
We solve the second part of the task in the same way. Since |−5|=5 and |−2|=2 , then (−5):(−2)=|−5|:|−2|=5:2 . This quotient corresponds to the common fraction 5/2, which can be written as a mixed number.
The same results are obtained if we use a different rule for dividing negative numbers. Indeed, the number −3 is the inverse number , then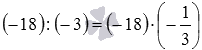 
, now we multiply negative numbers: 
. Likewise, .
Answer:
(−18):(−3)=6 and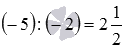 
.
When dividing fractional rational numbers, it is most convenient to work with ordinary fractions. But, if convenient, you can also divide finite decimal fractions.
Example.
Divide the number −0.004 by −0.25.
Solution.
The modules of the dividend and divisor are equal to 0.004 and 0.25, respectively, then according to the rule for dividing negative numbers we have (−0,004):(−0,25)=0,004:0,25 .
- or perform column division of decimal fractions,
- or go from decimals to ordinary fractions, and then divide the corresponding ordinary fractions.
Let's look at both approaches.
To divide 0.004 by 0.25 with a column, first move the decimal point 2 digits to the right, and we will arrive at dividing 0.4 by 25. Now we do the division by column: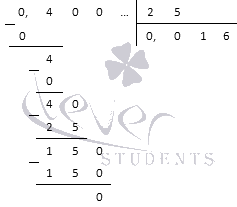 
Thus, 0.004:0.25=0.016.
Now let’s show what the solution would look like if we decided to convert decimal fractions to ordinary fractions. Because 
and , then 
, and execute
Dividing negative numbers has the same meaning as dividing positive numbers: using a given product and one of the factors, the second factor is found.
For example, dividing -12 by -4 means finding a number x such that -4's = -12. First, let's find the sign of the number x. Since multiplying -4 by x resulted in a negative number -12, the factors -4 and x must have different signs. Therefore x - positive number. Now let's find the modulus of the number x. Since the product modulus equal to the product moduli of multipliers, then |-12| = |-4| |x|. Hence |x| = |-12| : |-4|. But since x is a positive number, then x = |x|. So x = 3.
They write: (-12) : (-4) = |-12| : |-4| = 3, or shorter:
(-12) : (-4) = 12:4 = 3.
- To divide a negative number by a negative number, you need to divide the modulus of the dividend by the modulus of the divisor.
For example, -4.5: (-1.5) = 4.5: 1.5 = 3;
Dividing -24 by 4 means finding a number x such that 4 = -24. When multiplying 4 by x, the result is a negative number -24, which means that the factors 4 and x must have different signs. Therefore x is a negative number. In this case the equality |4| |x| = |-24|.
Hence |x| = |-24| : |4| = 24: 4 = 6. This means that x is a negative number with modulus 6, i.e. x = -6.
So -24:4 = -6.
Reasoning in the same way, we get that 24: (-4) = -6.
- When dividing numbers with different signs, necessary:
1) divide the module of the dividend by the module of the divisor;
2) put a “-” sign in front of the resulting number.
Usually, the sign of the quotient is first determined and written, and then the module of the quotient is found.
For example, 3.6: (-3) = -(3.6: 3) = -1.2;
When zero is divided by any number not equal to zero, the result is zero. You can't divide by zero!
Formulate the rule for dividing a negative number by a negative number.
Formulate a rule for dividing numbers with different signs.
What is the quotient 0: a, where a ≠ 0?
1149. Is the division done correctly:
1150. Find the quotient:
1151. Perform division:
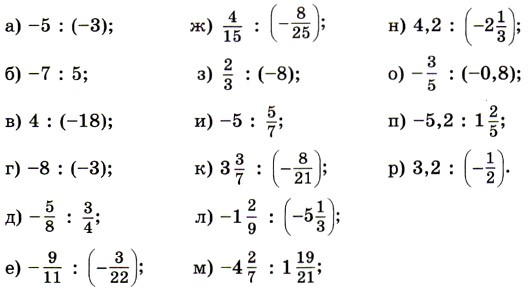
1152. Follow these steps:
1153. Find the meaning of the expression:
a) (3m + 6m) : 9, if m = -12; -5.96;
b) (5.2a - 5.2b): 5.2, if a = -27, b = -3.64.
1154. What is the quotient equal to:
1155. Solve the equation and check:
1157. I thought of a number, multiplied it by 5, and then subtracted 2.7 from the product. The result was -21.7. What number did I have in mind?
1158. Find the meaning of the expression:
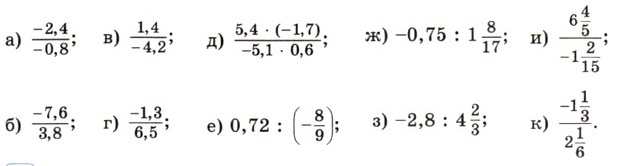
1159. Find the unknown term of the proportion:
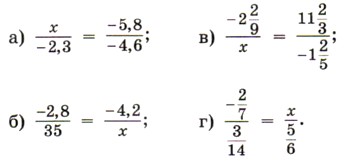
1160. Calculate orally:
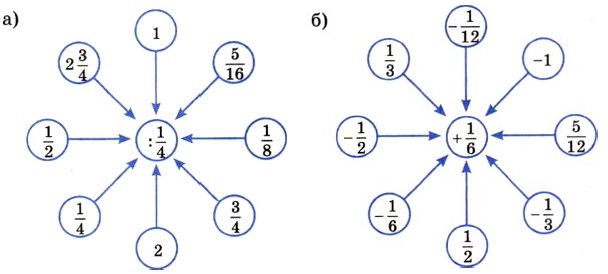
1161. At what values of the factors does the product xy equal zero? not equal to zero?
1162. In what cases can the equality be true: a) x = x 2 ; b) x = x 3; c) x 2 = x 3?
1163. Check the validity of the equality |ab| using examples. = |a| |b|. Try to prove that this equality is true for any values of a and b.
1164. Calculate:
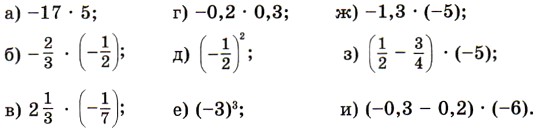
1165. Imagine the numbers 9; 16 and 25 as a product of two equal factors. In how many ways can this be done?
1166. Find the meaning of the expression:
a) -2.3 0.1 + 35 (-0.01) - (-2.1) (-0.2);
b) (4.8 - 7.3 + 2.1 - 2.7 + 3.1) (-183).
1167. Figure 90 shows a world map with time zones. Using it, determine: a) standard time in Yekaterinburg and Vladivostok, if it is midnight in Moscow; b) standard time in London, Tokyo, New York and
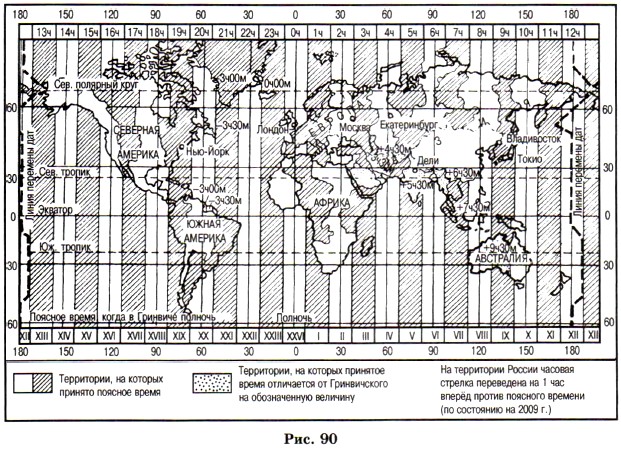
Delhi, if it’s 11 am in Moscow. Make up your own and solve several problems to determine standard time.
1168. Kostya and Vera left at the same time from the same point in the same direction. Kostya walks at a speed of a km/h, and Vera walks at a speed of b km/h. What will be the distance between them after t hours? Write a formula for solving the problem, denoting the required distance (in kilometers) with the letter s and knowing that a > b. Find it using the formula:
1169. Solve the previous problem by replacing the words “in the same direction” with the words “in opposite directions.” Find using the resulting formula:
1170. For what integer values of x is the inequality true:
1171. Calculate using a microcalculator:
a) -3.82 0.375 - 3.8275; b) 4.15 (-1.236) + 3.0994.
1172. Perform division:
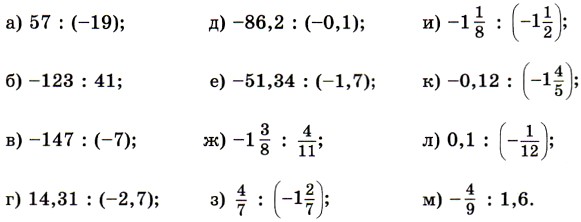
1173. Solve the equation:
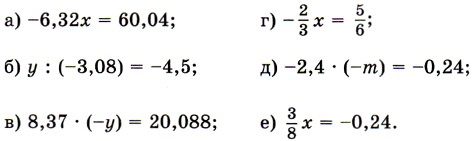
1174. Find the meaning of the expression:
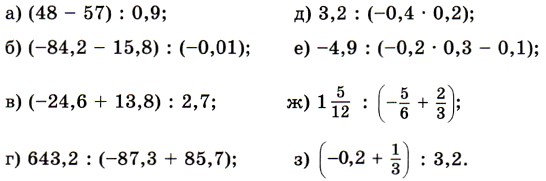
1175. Two motorcyclists left the city at the same time in the same direction. The speed of the first of them was greater than the speed of the second and amounted to 72 km/h. After 25 minutes, the distance between the motorcyclists was 5 km. Find the speed of the second motorcyclist.
1176. Find the meaning of the expression:
1177. Solve the equation:
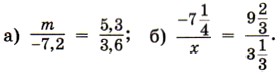
Goals:
- teach how to divide positive and negative numbers
- reinforce addition, subtraction and multiplication of positive and negative numbers
- develop competent mathematical speech
- develop interest in the subject
Equipment: PC, multimedia projector.
Lesson progress
Teacher: Hello, please sit down. Today we will study new material with you, but from the beginning we will repeat previously studied material. To do this we will need to solve examples.
1. Oral exercises
| A) | |
| b) |  |
| V) |  |
| G) | |
| d) |  |
| e) |  |
| and) |
2. Work on the topic of the lesson
(Slides 8–14)
1. Division of negative numbers has the same meaning as division of positive numbers, i.e. Using this product and one of the factors, the second factor is found.
Who can name the components of fission?
For example: -10: (-5) = ?
What does -10: (-5) mean? (So, find a number x such that at -5 x = -10)
Now let's find the sign of the number X.
How do you think this can be done?
Since when multiplying -5 by X the result is a negative number -10, therefore the factors must have different signs. Hence, X is a positive number.
Now let's find the modulus of the number X.
Since the modulus of the product is equal to the product of the moduli of the factors, therefore . Hence 
, because X is a positive number, then x = investigator X =
2
It is written like this:
or shorter
(-10) : (-5) = 10: 5 = 2
Rule: to divide a negative number by a negative number, you must divide the modulus of the dividend by the modulus of the divisor.
2.2. Now let's divide the negative number by the positive one.
For example: -24:4 =?
What does -24:4 mean? (So, find such a number X, that at 4 · X = -24)
Now let's find the sign of the number x.
How can this be done?
Since multiplying 4 by x produces a negative number -24, therefore X– negative number.
Now let's find the modulus of the number X.
What do you think it will be equal to?
hence
because X is a negative number with modulus 6, then X will be equal to -6
We get: -24: 4 = -6
It turns out similarly when dividing 24: (-4) = -6
Now let's talk about the algorithm for dividing numbers with different signs. So:
- divide the module of the dividend by the module of the divisor;
- put a minus sign in front of the resulting number.
3. When zero is divided by any number not equal to zero, the result is zero.
And the most important rule: You cannot divide by zero!
3. Consolidation of new material
(Slides 15–16).
| 1) | |
| 2) |  |
| 3) |  |
| 4) |  |
| 5) |  |
| 6) |  |
2. Independent work. This work will take you 8-10 minutes.
(Slides 17–24)
| A) | -4 (-5) – (-30) : 6 = 25 |
| b) | 15: (-15) – (-24) : 8 = 2 |
| V) | -8 (-3 + 12) : 36 + 2 = 0 |
| G) | 2,3 (-6 – 4) : 5 = - 4,6 |
| d) | (-8 + 32) : (-6) – 7 = -11 |
| e) | -21 + (-3 - 4 + 5) : (-2) = - 20 |
| and) | -6 4 – 64: (-3,3 + 1,7) = - 64 |
| h) | (-6 + 6,4 – 10) : (-8) (-3) = - 3 |
