This article provides a detailed overview dividing numbers with different signs . First, the rule for dividing numbers with different signs is given. Below are examples of dividing positive numbers by negative and negative numbers to positive.
Page navigation.
Rule for dividing numbers with different signs
In the article division of integers, a rule for dividing integers with different signs was obtained. It can be extended to both rational numbers and real numbers by repeating all the reasoning from the above article.
So, rule for dividing numbers with different signs has the following wording: to divide positive number for a negative number or a negative number for a positive one, you must divide the dividend by the modulus of the divisor, and put a minus sign in front of the resulting number.
Let's write this division rule using letters. If the numbers a and b have different signs, then the formula is valid a:b=−|a|:|b| .
From the stated rule it is clear that the result of dividing numbers with different signs is a negative number. Indeed, since the modulus of the dividend and the modulus of the divisor are positive numbers, their quotient is a positive number, and the minus sign makes this number negative.
Note that the rule considered reduces the division of numbers with different signs to the division of positive numbers.
You can give another formulation of the rule for dividing numbers with different signs: to divide the number a by the number b, you need to multiply the number a by the number b −1, the inverse of the number b. That is, a:b=a b −1 .
This rule can be used when it is possible to go beyond the set of integers (since not every integer has an inverse). In other words, it applies to the set of rational numbers as well as the set of real numbers.
It is clear that this rule for dividing numbers with different signs allows you to move from division to multiplication.
The same rule is used when dividing negative numbers.
It remains to consider how this rule for dividing numbers with different signs is applied when solving examples.
Examples of dividing numbers with different signs
Let us consider solutions to several characteristic examples of dividing numbers with different signs to understand the principle of applying the rules from the previous paragraph.
Example.
Divide the negative number −35 by the positive number 7.
Solution.
The rule for dividing numbers with different signs prescribes first finding the modules of the dividend and divisor. The modulus of −35 is 35, and the modulus of 7 is 7. Now we need to divide the module of the dividend by the module of the divisor, that is, we need to divide 35 by 7. Remembering how division of natural numbers is performed, we get 35:7=5. The last step left in the rule for dividing numbers with different signs is to put a minus in front of the resulting number, we have −5.
Here's the whole solution: .
It was possible to proceed from a different formulation of the rule for dividing numbers with different signs. In this case, we first find the inverse of the divisor 7. This number is the common fraction 1/7. Thus, . It remains to multiply numbers with different signs: . Obviously, we came to the same result.
Answer:
(−35):7=−5 .
Example.
Calculate the quotient 8:(−60) .
Solution.
According to the rule for dividing numbers with different signs, we have 8:(−60)=−(|8|:|−60|)=−(8:60)
. The resulting expression corresponds to a negative ordinary fraction (see the division sign as a fraction bar), you can reduce the fraction by 4, we get 
.
Let's write down the whole solution briefly: .
Answer:
.
When dividing fractional rational numbers with different signs, their dividend and divisor are usually represented as ordinary fractions. This is due to the fact that it is not always convenient to perform division with numbers in other notation (for example, in decimal).
Example.
Solution.
The module of the dividend is equal to , and the module of the divisor is equal to 0,(23) . To divide the modulus of the dividend by the modulus of the divisor, let's move on to ordinary fractions.
Let's convert a mixed number to an ordinary fraction: 
, and also convert the periodic decimal fraction into an ordinary fraction: .
Thus, .
Now let's deal with multiplication and division.
Let's say we need to multiply +3 by -4. How to do this?
Let's consider such a case. Three people are in debt and each has $4 in debt. What is the total debt? In order to find it, you need to add up all three debts: 4 dollars + 4 dollars + 4 dollars = 12 dollars. We decided that the addition of three numbers 4 is denoted as 3x4. Since in in this case we are talking about debt, there is a “-” sign before the 4. We know that the total debt is $12, so our problem now becomes 3x(-4)=-12.
We will get the same result if, according to the problem, each of the four people has a debt of $3. In other words, (+4)x(-3)=-12. And since the order of the factors does not matter, we get (-4)x(+3)=-12 and (+4)x(-3)=-12.
Let's summarize the results. When you multiply one positive number and one negative number, the result will always be a negative number. The numerical value of the answer will be the same as in the case of positive numbers. Product (+4)x(+3)=+12. The presence of the “-” sign only affects the sign, but does not affect the numerical value.
How to multiply two negative numbers?
Unfortunately, it is very difficult to come up with a suitable real-life example on this topic. It is easy to imagine a debt of 3 or 4 dollars, but it is absolutely impossible to imagine -4 or -3 people who got into debt.
Perhaps we will go a different way. In multiplication, when the sign of one of the factors changes, the sign of the product changes. If we change the signs of both factors, we must change twice work mark, first from positive to negative, and then vice versa, from negative to positive, that is, the product will have an initial sign.
Therefore, it is quite logical, although a little strange, that (-3) x (-4) = +12.
Sign position when multiplied it changes like this:
- positive number x positive number = positive number;
- negative number x positive number = negative number;
- positive number x negative number = negative number;
- negative number x negative number = positive number.
In other words, multiplying two numbers with the same signs, we get a positive number. Multiplying two numbers with different signs, we get a negative number.
The same rule is true for the action opposite to multiplication - for.
You can easily verify this by running inverse multiplication operations. In each of the examples above, if you multiply the quotient by the divisor, you will get the dividend and make sure it has the same sign, for example (-3)x(-4)=(+12).
Since winter is coming, it’s time to think about what to change your iron horse’s shoes into, so as not to slip on the ice and feel confident on the ice. winter roads. You can, for example, buy Yokohama tires on the website: mvo.ru or some others, the main thing is that they are of high quality, you can find out more information and prices on the website Mvo.ru.
In this article we will deal with multiplying numbers with different signs. Here we will first formulate the rule for multiplying positive and negative numbers, justify it, and then consider the application of this rule when solving examples.
Page navigation.
Rule for multiplying numbers with different signs
Multiplying a positive number by a negative number, as well as a negative number by a positive number, is carried out as follows: the rule for multiplying numbers with different signs: to multiply numbers with different signs, you need to multiply and put a minus sign in front of the resulting product.
Let's write this rule down in letter form. For any positive real number a and any negative real number −b, the following equality holds: a·(−b)=−(|a|·|b|) , and also for a negative number −a and a positive number b the equality (−a)·b=−(|a|·|b|) .
The rule for multiplying numbers with different signs is fully consistent with properties of operations with real numbers. Indeed, on their basis it is easy to show that for real and positive numbers a and b a chain of equalities of the form a·(−b)+a·b=a·((−b)+b)=a·0=0, which proves that a·(−b) and a·b are opposite numbers, which implies the equality a·(−b)=−(a·b) . And from it follows the validity of the multiplication rule in question.
It should be noted that the stated rule for multiplying numbers with different signs is valid both for real numbers and for rational numbers and for integers. This follows from the fact that operations with rational and integer numbers have the same properties that were used in the proof above.
It is clear that multiplying numbers with different signs according to the resulting rule comes down to multiplying positive numbers.
It remains only to consider examples of the application of the disassembled multiplication rule when multiplying numbers with different signs.
Examples of multiplying numbers with different signs
Let's look at several solutions examples of multiplying numbers with different signs. Let's start with a simple case to focus on the steps of the rule rather than the computational complexity.
Example.
Multiply the negative number −4 by the positive number 5.
Solution.
According to the rule for multiplying numbers with different signs, we first need to multiply the modules of the original factors. The modulus of −4 is equal to 4, and the modulus of 5 is equal to 5, and multiplying the natural numbers 4 and 5 gives 20. Finally, it remains to put a minus sign in front of the resulting number, we have −20. This completes the multiplication.
Briefly, the solution can be written as follows: (−4) 5=−(4 5)=−20.
Answer:
(−4)·5=−20.
When multiplying fractions with different signs, you need to be able to multiply ordinary fractions, multiply decimals and their combinations with natural and mixed numbers.
Example.
Multiply numbers with different signs 0, (2) and .
Solution.
By converting a periodic decimal fraction into a common fraction, and also by converting from a mixed number to an improper fraction, from the original product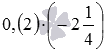 
we will come to the product of ordinary fractions with different signs of the form . This product, according to the rule of multiplying numbers with different signs, is equal to . All that remains is to multiply common fractions in parentheses, we have 
.
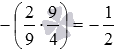Answer:
.
Separately, it is worth mentioning the multiplication of numbers with different signs, when one or both factors are
