Have you ever been amazed by people who can easily add and multiply three-digit numbers in their heads or instantly name the root of 729?
In fact, it is not as difficult as it seems, it’s just that here, as in any skill, you need knowledge of technique and regular training. Well, training depends only on you, and now we’ll look at the technique.
Let's start with adding two-digit numbers.
Let us need to calculate 37 + 85 + 29 + 42 . To do this, first add up all the tens: 3 + 8 + 2 + 4. Note that 8 + 2 = 10, 3 + 4 = 7, together 17. Remember. Now we add the units: 7 + 5 + 9 + 2 = 23.
17 tens is 170. 170 + 23 = 193. As you can see, this is faster than adding 37 and 85, then adding 29, etc.
By the way, the same can be done if we add three-digit numbers.
For example: 228 + 39 + 485 + 91.
Adding up tens:
22 + 3 + 48 + 9 = (22 + 48) + (3 + 9) = 70 + 12 = 82.
Now we add the units:
8 + 9 + 5 + 1 = (8 + 5) + (9 + 1) = 13 + 10 = 23.
(If two numbers add up to ten, it is always convenient to add them first).
Well, now there are 82 tens, i.e. 820 plus 23 is 843.
Now let's move on to more interesting topic –multiplying two-digit numbers. Here we will also act unusually. The technique that we will now consider is called “cross” multiplication or Hindu method of multiplication.
We want to multiply 76 by 28. We proceed as follows:
First, let's multiply the units: 6 8 = 48,
now we multiply with a cross 7 8 + 2 6 = 56 + 12 = 68 tens, and taking into account 4 tens from the number 48, we have 72 tens and 8 units or 720 and 8. Now multiply hundreds: 7 2 = 14 hundreds or taking into account 7 hundreds from the number 720 we have 21 hundreds, 2 tens and 8 units. Answer: 2128.
We've looked at a method that works for any two-digit numbers, but often the calculations can be simplified by noticing certain features of our factors.
For example, in our case, 76 is nothing more than 75 + 1.
Then: 28 76 = 28 (75 + 1) = 28 75 + 28 = 28 (50 + 25) + 28 = 28 50 + 28 25 + 28 = 2800/2 + 1400/2 + 28 =
1400 + 700 + 28 = 2128
Of course, we do not write out all these calculations, but perform them in our heads. They, like the figure with a cross, are shown in order to show the multiplication algorithm. In fact, all calculations are carried out “in the mind.” Yes, at first the calculations using this method may seem complicated, but we do not forget about the second component of success - practice. A little practice and everything will work out!
Well, for inquisitive “theorists” we will show how this method was invented.
Let's consider multiplying two two-digit numbers in general form: multiply ab by cd.
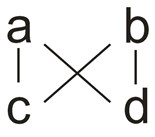
We can always write ab as a · 10 + b and cd as c · 10 + d. Then:
(a 10 + b)(c 10 + d) =
100 a c + 10 a d + 10 b c + b d =
A c 100 + (a d + b c) 10 + b d
From the result of multiplication it is clear that in order to get hundreds it is necessary to multiply the first digits of our numbers, to get tens we multiply them with a cross and add them, and finally, multiplying the last digits gives us the number of units.
www.site, when copying material in full or in part, a link to the original source is required.
The process of mental counting can be considered as a counting technology that combines human ideas and skills about numbers and mathematical arithmetic algorithms.
There are three types mental counting technologies, which use various physical capabilities of a person:
audiomotor counting technology;
visual counting technology.
Characteristic feature audiomotor mental counting is to accompany each action and each number with a verbal phrase like “twice two is four.” The traditional counting system is precisely an audiomotor technology. The disadvantages of the audiomotor method of calculations are:
absence of relationships in the memorized phrase with neighboring results,
the inability to separate tens and units of a product in phrases about the multiplication table without repeating the entire phrase;
the inability to reverse the phrase from the answer to the factors, which is important for performing division with a remainder;
slow speed of reproduction of a verbal phrase.
Supercomputers, demonstrating high speed of thinking, use their visual abilities and excellent visual memory. People who are good at speed calculations do not use words when solving an arithmetic example in their head. They demonstrate reality visual technology of mental counting, devoid of the main drawback - the slow speed of performing basic operations with numbers.
Perhaps our methods of multiplication are not perfect; Maybe an even faster and more reliable one will be invented.
Of course, it is impossible to know all the methods of quick counting, but the most accessible ones can be studied and applied.
Mental counting training.
There are people who can perform simple arithmetic operations in their heads. Multiply two-digit number by a single digit, multiply within 20, multiply two small two-digit numbers, etc. - they can perform all these actions in their minds and quite quickly, faster than the average person. Often this skill is justified by the need for constant practical use. Typically, people who are good at mental arithmetic have a background in mathematics or at least experience solving numerous arithmetic problems.
Undoubtedly, experience and training play a vital role in the development of any ability. But the skill of mental calculation does not rely on experience alone. This is proven by people who, unlike those described above, are able to count in their minds much more complex examples. For example, such people can multiply and divide three-digit numbers, perform complex arithmetic operations that not every person can count in a column.
What does an ordinary person need to know and be able to do in order to master such a phenomenal ability? Today, there are various techniques that help you learn how to quickly count in your head. Having studied many approaches to teaching the skill of counting orally, we can highlight3 main components of this skill:
1. Abilities. The ability to concentrate and the ability to hold several things in short-term memory at the same time. Predisposition to mathematics and logical thinking.
2. Algorithms. Knowledge of special algorithms and the ability to quickly select the necessary, most effective algorithm in each specific situation.
3. Training and experience, the importance of which for any skill has not been canceled. Constant training and gradual complication of solved problems and exercises will allow you to improve the speed and quality of mental calculation.
It should be noted that the third factor is of key importance. Without the necessary experience, you will not be able to surprise others quick counting, even if you know the most convenient algorithm. However, do not underestimate the importance of the first two components, since having in your arsenal the abilities and a set of necessary algorithms, you can “outdo” even the most experienced “accountant”, provided that you have trained for the same amount of time.
Several ways to count mentally:
1. Multiply by 5 It’s more convenient to do this: first multiply by 10, and then divide by 2
2. Multiply by 9. In order to multiply a number by 9, you need to add 0 to the multiplicand and subtract the multiplicand from the resulting number, for example 45 9 = 450-45 = 405.
3. Multiply by 10. Add a zero to the right: 48 10 = 480
4. Multiply by 11. two-digit number. Spread the numbers N and A, enter the amount in the middle (N+A).
for example, 43 11 = = = 473.
5. Multiply by 12. is done in approximately the same way as for 11. We double each digit of the number and add to the result the neighbor of the original digit on the right.
Examples.Let's multiplyon.
Let's start with the rightmost number - this is. Let's double itand add a neighbor (he is not in in this case). We get. Let's write it downand remember.
Let's move left to the next number. Let's double it, we get, add a neighbor,, we get, add. Let's write it downand remember.
Let's move left to the next number,. Let's double it, we get. Let's add a neighborand we get. Let's add, which we remembered, we get. Let's write it downand remember.
Let's move to the left to a non-existent number - zero. Let's double it, get and add a neighbor, which will give us . Finally, we add , which we remembered, and we get . Let's write it down. Answer: .
6. Multiplication and division by 5, 50, 500, etc.
Multiplication by 5, 50, 500, etc. is replaced by multiplication by 10, 100, 1000, etc., followed by division by 2 of the resulting product (or division by 2 and multiplication by 10, 100, 1000, etc. ). (50 = 100: 2, etc.)
54 5=(54 10):2=540:2=270 (54 5 = (54:2) 10= 270).
To divide a number by 5.50, 500, etc., you need to divide this number by 10,100,1000, etc. and multiply by 2.
10800: 50 = 10800:100 2 =216
10800: 50 = 10800 2:100 =216
7. Multiplication and division by 25, 250, 2500, etc.
Multiplication by 25, 250, 2500, etc. is replaced by multiplication by 100, 1000, 10000, etc. and the resulting result is divided by 4. (25 = 100: 4)
542 25=(542 100):4=13550 (248 25=248: 4 100 = 6200)
(if the number is divisible by 4, then multiplication does not take time; any student can do it).
To divide a number by 25, 25,250,2500, etc., this number must be divided by 100,1000,10000, etc. and multiply by 4: 31200: 25 = 31200:100 4 = 1248.
8. Multiplication and division by 125, 1250, 12500, etc.
Multiplication by 125, 1250, etc. is replaced by multiplication by 1000, 10000, etc. and the resulting product must be divided by 8. (125 = 1000 : 8)
72 125=72 1000: 8=9000
If the number is divisible by 8, then first divide by 8, and then multiply by 1000, 10000, etc.
48 125 = 48: 8 1000 = 6000
To divide a number by 125, 1250, etc., you need to divide this number by 1000, 10000, etc. and multiply by 8.
7000: 125 = 7000: 10008 = 56.
9. Multiplication and division by 75, 750, etc.
To multiply a number by 75, 750, etc., you need to divide this number by 4 and multiply by 300, 3000, etc. (75 = 300:4)
4875 = 48:4300 = 3600
To divide a number by 75,750, etc., you need to divide this number by 300, 3000, etc. and multiply by 4
7200: 75 = 7200: 3004 = 96.
10. Multiply by 15, 150.
When multiplying by 15, if the number is odd, multiply it by 10 and add half of the resulting product:
23 15=23 (10+5)=230+115=345;
if the number is even, then we proceed even simpler - we add half of it to the number and multiply the result by 10:
18 15=(18+9) 10=27 10=270.
When multiplying a number by 150, we use the same technique and multiply the result by 10, since 150 = 15 10:
24 150=((24+12) 10) 10=(36 10) 10=3600.
In the same way, quickly multiply a two-digit number (especially an even one) by a two-digit number ending in 5:
24 35 = 24 (30 +5) = 24 30+24:2 10 = 720+120=840.
11. Multiplying two-digit numbers less than 20.
To one of the numbers you need to add the number of units of the other, multiply this amount by 10 and add to it the product of the units of these numbers:
18 16=(18+6) 10+8 6= 240+48=288.
Using the described method, you can multiply two-digit numbers less than 20, as well as numbers that have the same number of tens: 23 24 = (23+4) 20+4 6=27 20+12=540+12=562.
Explanation:
(10+a) (10+b) = 100 + 10a + 10b + a b = 10 (10+a+b) + a b = 10 ((10+a)+b) + a b .
12. Multiplying a two-digit number by 101 .
Perhaps the simplest rule: assign your number to yourself. Multiplication is complete.
Example: 57 101 = 5757 57 --> 5757
Explanation: (10a+b) 101 = 1010a + 101b = 1000a + 100b + 10a + b
Similarly, three-digit numbers are multiplied by 1001, four-digit numbers by 10001, etc.
13. Multiplication by 22, 33, ..., 99.
To multiply a two-digit number 22.33, ...,99, you need to represent this factor as the product of a single-digit number by 11. First multiply by single digit number, and then at 11:
15 33= 15 3 11=45 11=495.
14. Multiplying two-digit numbers by 111 .
First, let’s take as a multiplicand a two-digit number whose sum of digits is less than 10. Let’s explain with numerical examples:
Since 111=100+10+1, then 45 111=45 (100+10+1). When multiplying a two-digit number, the sum of the digits of which is less than 10, by 111, it is necessary to insert twice the sum of the digits (i.e., the numbers represented by them) of its tens and units 4+5=9 into the middle between the digits. 4500+450+45=4995. Therefore, 45,111=4995. When the sum of the digits of a two-digit multiplicand is greater than or equal to 10, for example 68 11, you need to add the digits of the multiplicand (6+8) and insert 2 units of the resulting sum into the middle between the numbers 6 and 8. Finally, add 1100 to the composed number 6448. Therefore, 68 111 = 7548.
15. Squaring numbers consisting of only 1.
11 x 11 =121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 =123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
Some non-standard multiplication techniques.
Multiplying a number by a single-digit factor.
To multiply a number by a single-digit factor (for example, 34 9) orally, you must perform actions starting from the highest digit, sequentially adding the results (30 9=270, 4 9=36, 270+36=306).
For effective mental counting, it is useful to know the multiplication table up to 19*9. In this case, multiplication is 147 8 is performed in the mind like this: 147 8=140 8+7 8= 1120 + 56= 1176 . However, without knowing the multiplication table up to 19 9, in practice it is more convenient to calculate all such examples by reducing the multiplier to the base number: 147 8=(150-3) 8=150 8-3 8=1200-24=1176, with 150 8=(150 2) 4=300 4=1200.
If one of the multiplied items is decomposed into single-digit factors, it is convenient to perform the action by sequentially multiplying by these factors, for example, 225 6=225 2 3=450 3=1350. Also, it may be easier to use 225 6=(200+25) 6=200 6+25 6=1200+150=1350.
Multiplying two-digit numbers.
1. Multiply by 37.
When multiplying a number by 37, if the given number is a multiple of 3, it is divided by 3 and multiplied by 111.
27 37=(27:3) (37 3)=9 111=999
If the given number is not a multiple of 3, then 37 is subtracted from the product or 37 is added to the product.
23 37=(24-1) 37=(24:3) (37 3)-37=888-37=851.
It is easy to remember the product of some of them:
3 x 37 = 111 33 x 3367 = 111111
6 x 37 = 222 66 x 3367 = 222222
9 x 37 = 333 99 x 3367 = 333333
12 x 37 = 444 132 x 3367 = 444444
15 x 37 = 555 165 x 3367 = 555555
18 x 37 = 666 198 x 3367 = 666666
21 x 37 = 777 231 x 3367 = 777777
24 x 37 = 888 264 x 3367 = 888888
27 x 37 = 999 297 x 3367 = 99999
2. If tens of two-digit numbers begin with the same digit, and the sum of the ones is 10 , then when multiplying them we find the product in this order:
1) multiply the ten of the first number by the ten of the second larger number by one;
2) multiply the units:
8 3x 8 7= 7221 ( 8x9=72 , 3x7=21)
5 6x 5 4=3024 ( 5x6=30 , 6x4=24)
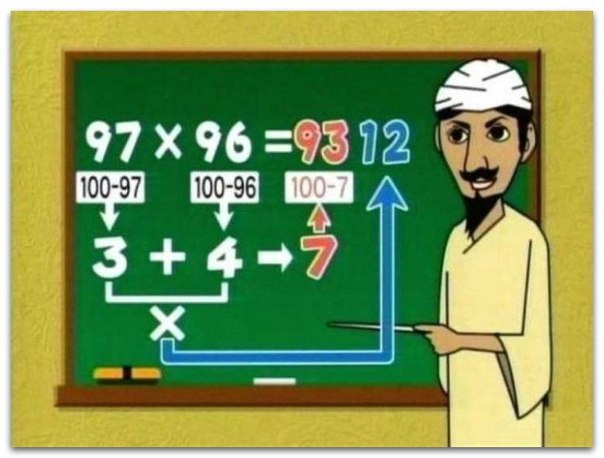
Algorithm for multiplying two-digit numbers close to 100
For example:97 x 96 = 9312
Here I use the following algorithm: if you want to multiply two
double-digit numbers close to 100, then do this:
1) find the disadvantages of factors up to a hundred;
2) subtract from one factor the deficiency of the second to a hundred;
3) add two digits to the result of the product of the shortcomings
factors up to hundreds.
The relevant literature mentions such methods of multiplication as “folding”, “lattice”, “back to front”, “diamond”, “triangle” and many others. I wanted to know what other non-standard multiplication techniques exist in mathematics? It turns out there are a lot of them. Here are some of these techniques.
Peasant method:
One of the multipliers is doubled, while the other is simultaneously decreased by the same amount. When the quotient becomes equal to one, the product obtained in parallel is the desired answer.
If the quotient turns out to be an odd number, then one is removed from it and the remainder is divided. Then the products that stood opposite the odd quotients are added to the answer received

"Method of the Cross"
In this method, the factors are written one below the other and their digits are multiplied in a straight line and crosswise.

3 1 = 3 – last digit.
2 1 + 3 3 = 11. The penultimate digit is 1, another 1 in the mind.
2 3 = 6; 6 + 1 = 7 is the first digit of the product
The required work is 713.
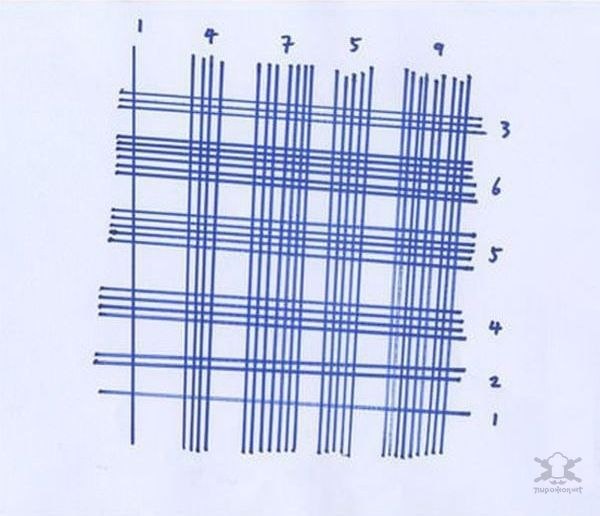
Sino-Japanese multiplication method.
It's no secret that in different countries teaching methods are different. It turns out that in Japan, first grade students can multiply three-digit numbers without knowing the multiplication table. For this it is used. The logic of the method is clear from the figure. After drawing, you just need to count the number of intersections in each area. 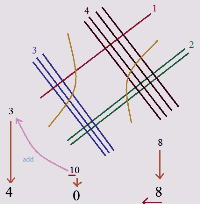

This method can be used to multiply even three-digit numbers. It is likely that when children later learn the multiplication tables, they will be able to multiply in a simpler and in a fast way, in a column. Moreover, the above method is too labor-intensive when multiplying numbers like 89 and 98, because you have to draw 34 stripes and count all the intersections. On the other hand, in such cases you can use a calculator. Many people will think that this method of Japanese or Chinese multiplication is too complicated and confusing, but this is only at first glance. It is visualization, that is, the image of all the points of intersection of lines (factors) on one plane, that gives us visual support, while the traditional method of multiplication involves a large number of arithmetic operations only in the mind. Chinese or Japanese multiplication not only helps you quickly and efficiently multiply two-digit and three-digit numbers by each other without a calculator, but also develops erudition. Agree, not everyone can boast that in practice they know the ancient Chinese method of multiplication (), which is relevant and works great in modern world.
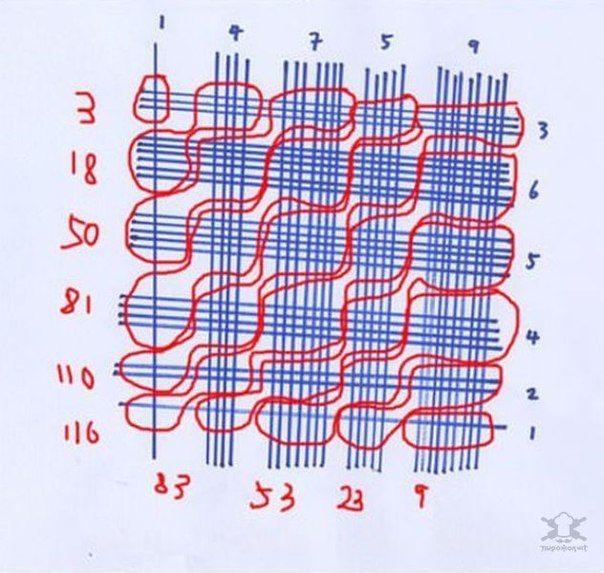
Multiplication can be done using a matrix table ts :
43219876=?
First we write the products of numbers.2. Find the sums along the diagonal:
36, 59, 70, 70, 40, 19, 6
3. We get the answer from the end by adding the “extra” digits to the leading digit:2674196
Lattice method.
A rectangle is drawn, divided into squares. Next are square cells, divided diagonally. In each line we will write the product of the numbers above this cell and to the right of it, while we will write the tens digit of the product above the slash, and the units digit below it. Now we add the numbers in each oblique strip, performing this operation, from right to left. If it turns out to be greater than 10, then we write only the units digit of the sum, and add the tens digit to the next sum.
65
2
4
1 7
3
7
7
We write the answer numbers from left to right: 4, 5, 17, 20, 7, 5. Starting from the right, we write, adding “extra” numbers to the “neighbor”: 469075.
Received: 725 x 647 = 469075.
Quick counting without a calculator. Fast counting techniques.

Let's consider some methods of quick mental calculation that are designed for the mind of an “ordinary” person and do not require unique abilities.


ADDITION
The basic rule for doing addition in your head is:
To add 9 to a number, add 10 to it and subtract 1; to add 8, add 10 and subtract 2; to add 7, add 10 and subtract 3, etc.
For example, 56+8=56+10-2=64;
65+9=65+10 -1=74.

ADDING TWO-DIGIT NUMBERS IN THE MIND
If the units digit in the number being added is greater than 5, then the number must be rounded up, and then the rounding error must be subtracted from the resulting amount.
If the number of units is less, then we add tens first, and then units.
For example, 34+48=34+50 – 2 = 82;
27+31=27+30+1 =58.

ADDING THREE-DIGIT NUMBERS
We add from left to right, that is, first hundreds, then tens, and then ones.
For example, 359+523= 300+500+50+20+9+3=
=800 +70 +12 = 882;
456+298=400+200+50+90+6+8=600+140+14=754 .

SUBTRACTION
To subtract two numbers in your head, you need to round up the subtrahend, and then adjust the answer you get.
For example, 56 – 9 = 56 – 10 + 1 = 47;
436 – 87 = 436 - 100 + 13 = 349.

Subtraction from 1000
To subtract from 1000 you can use this simple rule:
Subtract all digits from 9 except the last one. And subtract the last digit from 10:
For example, 1000 - 648
Step1: subtract 6 from 9 = 3
Step2: subtract 4 = 5 from 9
Step3: subtract 8 from 10 = 2
Answer: 352


Multiplying and dividing by 4.
To multiply a number by 4, it is doubled.
For example, 527 · 4 = (527 · 2) · 2 = 1054 · 2 = 2108.
To divide a number by 4, it is divided by 2 twice.
For example, 2648:4 = (2648:2):2 = 1324:2 = 662.

Multiplying and dividing by 5.
To multiply a number by 5, you need to multiply it by 10 and divide by 2.
For example, 348 · 5= (348 · 10) : 2 = 3480: 2 = 1740.
To divide a number by 5, you need to multiply it by 0.2, that is, in double the original number, separate the last digit with a comma.
For example, 51: 5 = 51 · 0,2 = 10,2.

Multiplying by a number ending in 5.
To multiply an even two-digit number by a number ending in 5, you should apply the rule: if one of the factors is increased several times and the other is decreased by the same amount, the product will not change.
For example,
44 · 5 = (44: 2) · 5 · 2 = 22 · 10 = 220;
26 · 35 = (26: 2) · 35 · 2 = 13 · 70 = 910;
36 · 45 = (36: 2) · 45 · 2 = 18 · 90 = 1625;
18 · 65 = (18: 2) · 65 · 2 = 9 · 130 = 1170;
12 · 75 = (12: 2) · 75 · 2 = 6 · 150 = 900;
14 · 85 = (14: 2) · 85 · 2 = 7 · 170 = 1190;
12 · 95 = (12: 2) · 95 · 2 = 6 · 190 = 1140.
When multiplying by 65, 75, 85, 95, numbers should be small, within the second ten. Otherwise the calculations will become more complicated.

Multiply by 25 .
To multiply a number by 25, you need to multiply it by 100/4, that is, multiply by 100 and divide by 4.
For example, 348 · 25 = (348 · 100) : 4 = (34800: 2) : 2 = 17400: 2 = 8700.
Multiply by 1.5.
To multiply a number by 1.5, you need to add half of it to the original number.
For example, 228 · 1,5 = 228 + 114 = 342.

Multiply by 9
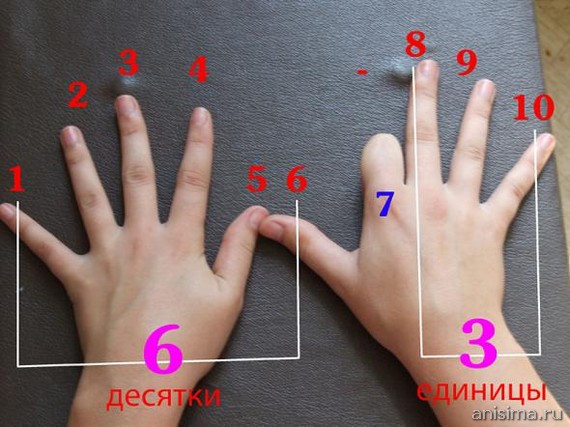
To multiply any number from 1 to 9 by 9, look at your hands.
Bend the finger that corresponds to the number being multiplied (for example, 9x3 - fold the third finger), count the fingers before the bent finger (in the case of 9x3, this is 2), then count after the bent finger (in our case, 7). Answer: 27.

Multiply by 9.
To multiply a number by 9, add 0 to it and subtract the original number.
For example, 847 · 9 = 8470 – 847 = 7623.

Multiplication multi-digit numbers by 9 .
1. Increase the number of tens by 1 and subtract it from the multiplicand.
2. We add to the result the addition of the units digit of the multiplicand to 10.
For example, 576 · 9
1. 576 – (57+1)=518
Answer: 5184
1. 379 – (37 + 1) =341
Answer: 3411

Multiply by 99
1. From a number, subtract the number of its hundreds, increased by 1.
2. Find the complement of the number formed by the last two digits to 100.
3. We assign an addition to the previous result.
Example:
27 99 134 99
27 – 1 = 26 (hundreds – 0+1) 134 – 2 = 132 (hundreds – 1 + 1)
100 - 27 = 73 100 – 34 = 66
27 99 = 2673 134 99 = 13266

Multiplying by 11 .
1 way. To multiply a number by 11, add 0 to it and add the original number.
For example, 243 · 11 = 2430 + 243 = 2673.
Method 2. If you want to multiply a number by 11, then do this: write down the number that needs to be multiplied by 11, and between the digits of the original number insert the sum of these digits.
If the sum turns out to be a two-digit number, then add 1 to the first digit of the original number.
For example, 45 11 = 4 (4+5)7= 967.

Multiply by 12.
To multiply a number by 12: you need to double each digit in turn and add its “neighbor” to it in turn.
For example, 63247 12
It is necessary to write down the digits of the multiplicand at intervals and write each digit of the result exactly under the digit of the number 63247 from which it was formed.
63247 · 12 twice 7 will = 14, carry over 1
63247 · 12 twice 4 + 7 + 1 = 16, carry over 1
63247 · 12 twice 2 + 4 + 1 = 9
The next steps are similar.
Final answer: 63247 · 12= 758964.

Multiplying by 22, 33, ..., 99.
To multiply a two-digit number by 22, 33, ..., 99, this factor must be represented as the product of a single-digit number by 11, that is, 44 = 4 · 11; 55 = 5 · 11.
Then multiply the product of the first numbers by 11:
For example, 24 22 = 24 2 11 = 48 11 = 528
23 66 =23 6 11=138 11=1518

Multiplication three-digit number on 101 .
To multiply a three-digit number by 101, we increase the first factor by the number of its hundreds and add the last two digits of the first factor to it on the right.
For example, 125 101 = 126(125+1)25 =12625
Children easily learn this technique when writing calculations in a column.

Squaring a number ending in 5 .
To square a number ending in 5 (for example, 65), multiply its tens number (6) by the number of tens increased by 1 (6+1 = 7), and add 25 to the resulting number
(6 7)25 = 4225
For example: 95 2 =(9 · 10)25= 9025; 125 2 = (12 13)25=15625
Squaring a number close to 50.
If you want to square a number that is close to 50 but greater than 50, then do this:
1) subtract 25 from this number;
2) add to the result in two digits the square of the excess of the given number over 50.
Examples:
1) 58 2 = 3364. Explanation: 58 – 25 = 33, 58-50 = 8, 8 2 = 64, 58 2 = 3364.
2) 67 2 = 4489. Explanation: 67 – 25 = 42, 67 – 50 = 17, 17 2 =289, 67 2 = 4200 + 289 = = 4489.
If you want to square a number that is close to 50 but less than 50, then do this :
1) subtract 25 from this number;
2) add to the result in two digits the square of the disadvantage of this number up to 50.
1) 48 2 = 2304. Explanation: 48 – 25 = 23, 50 – 48 =2, 2 2 = 4, 48 2 = 2304.
2) 37 2 = 1369. Explanation: 37 – 25 = 12, = 13, 13 2 = 169, 37 2 = 1200 + 169 = 1369.

Multiply by 37.
To multiply a number by 37, you need to divide this number by 3 and multiply by 111.
For example: 24 37 = (24: 3) 37 3 = 8 111 = 888;
27 · 37 = (27: 3) · 111 = 999.
Divide by 37.
To divide a number by 37, you need to divide this number by 111 and multiply by 3.
For example: 999: 37 = 999:111 · 3 = 27;
888: 37 = 888:111 · 3 = 24.
To learn how to verbally multiply and divide by 37, you need to have a good knowledge of the multiplication table by three and the sign of divisibility by three.

Multiplying two adjacent numbers
When multiplying two adjacent numbers, you must first multiply the tens digits, then multiply the tens digits by the sum of the ones digits, and finally, you must multiply the ones digits. We'll get the answer.
For example: 12×13
Step1. 1 × 1 = 1
Step 2. 1 × (2+3) = 5
Step 3. 2 × 3 = 6

Multiplying a pair of numbers whose tens digits are the same and the sum of their ones digits is 10
Example:
24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.
We round the numbers 24 and 26 to tens to get the number of hundreds, and add the product of units to the number of hundreds.
18 × 12 = 2 × 1 cell. + 8 × 2 = 200 + 16 = 216;
23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;
34 × 36 = 3 × 4 cells. + 4 × 6 = 1224;
71 × 79 = 7 × 8 cells. + 1 × 9 = 5609;
82 × 88 = 8 × 9 cells. + 2 × 8 = 7216.
More complex examples can be solved orally:
108 × 102 = 10 × 11 cells. + 8 × 2 = 11016;
204 × 206 = 20 × 21 cells. +4 × 6 = 42024;
802 × 808 = 80 × 81 cells. +2 × 8 = 648016.
Examination:

Multiplying numbers ending in 1.
When multiplying numbers ending in 1, you must first multiply the tens digits and write the sum of the tens digits under this number to the right of the resulting product, and then multiply 1 by 1 and write it even further to the right.
Adding it in a column, we get the answer.
1) 81 × 31 = ?
8 × 3 = 24
8 + 3 = 11
1 × 1 = 1
81 × 31 = 2511
2) 21 × 31 = ?
2 × 3 = 6
2 +3 = 5
1 × 1 = 1
21 × 31 = 651
3) 91 × 71 = ?
9 × 7 = 63
9 + 7 = 16
1 × 1 = 1
91 × 71 = 6461

Multiplying two-digit numbers in which the sum of the tens digits is 10 and the ones digits are the same.
Rule. When multiplying two-digit numbers. for which the sum of the tens digits is 10, and the ones digits are the same, you need to multiply the tens digits. and add the units digit, we get the number of hundreds and add the product of units to the number of hundreds.
Examples:
72 × 32 = (7 × 3 + 2) cells. + 2 × 2 = 2304;
64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;
53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;
18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;
24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;
63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;
35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

Conclusion.
As we see, quick counting is no longer a sealed secret, but a scientifically developed system. Once there is a system, it means it can be studied, it can be followed, it can be mastered.
All the methods of mental counting that we have considered indicate the long-term interest of scientists and ordinary people to the numbers game.
Using some of these methods in the classroom or at home, you can develop the speed of calculations, instill interest in mathematics, and achieve success in studying all school subjects.
Quick counting techniques without a calculator
Although it is believed that mathematics terrifies a significant part of the population, everyone can count money. And this is exactly what people far from mathematics can do. I remember my husband’s grandmother showing him the multiplication table for 9 on her fingers. No education, just a huge practice of selling radishes and strawberries at the market!
So, we read, immediately check and remember the calculation methods in our heads.
1. Multiply by 11
Multiplying by 11 is a little more difficult than multiplying by 10. The pattern here is this:
53 x 11 = 583
Step 1 - Add two digits of a two-digit number: 5 + 3 = 8
Step 2 - Place the result between two numbers of a two-digit number: 583
59 x 11 = 649
Step 1 - 5 + 9 = 14
Step 2 - Throw one to the left if the sum in the previous step was greater than 9: 5 + 1 = 6 (the second symbol remains on the right, in this case it is a four)
Step 3 - We have already transferred one to the first character, we got 6. Next we have 4 left, which we put in the center and add 9: 649
2. Fast squaring
This trick will help quickly square a two-digit number that ends in 5.
85 x 85 = 7225
Step 1 - Multiply the first digit by the first digit increased by one: 8 x (8 + 1) = 72
Step 2 - Add 25 to the resulting result: 7225
45 x 45 = 2025
Step 1 - 4 x (4 + 1) = 20
Step 2 - 2025
3. Multiply by 5
Most people remember the 5 times tables very easily, but when dealing with larger numbers it becomes more difficult. Or not? This technique is incredibly simple.
Take any number, divide by 2 (in other words, divide in half). If the result is a whole number, add a 0 at the end. If not, ignore the comma and add 5 at the end.
This always works:
2682×5 = (2682 / 2) & 5 or 0
2682 / 2 = 1341 (integer, so add 0)
13410
Let's try another example:
5887×5
2943.5 (fractional number, skip comma, add 5)
29435
It's simple. To multiply any number from 1 to 9 by 9, look at your hands. Bend the finger that corresponds to the number being multiplied (for example, 9x3 - bend the third finger), count the fingers before the bent finger (in the case of 9x3, this is 2), then count after the bent finger (in our case, 7). The answer is 27.


5. Multiply by 4
This is a very simple technique, although obvious only to some. The trick is to simply multiply by 2, and then multiply by 2 again:
58×4 = (58×2) + (58×2) = (116) + (116) = 232
6. Counting tips
If you need to leave a 15% tip, there is an easy way to do it.
Calculate 10% (divide the number by 10), and then add the resulting number to half of it and get the answer:
15% of $25 = (10% of 25) + ((10% of 25) / 2)
$2.50 + $1.25 = $3.75
And, as a consequence): to multiply a number by 1.5 you need to add half of it to the original number. For example,
34*1,5 = 34+17=51
125*1,5= 125+62,5=187,5
7. Complex multiplication
If you need to multiply big numbers, and one of them is even, you can simply rearrange them to get the answer:
32x125 is the same as:
16x250 is the same as:
8x500 is the same as:
4x1000 = 4,000
8. Division by 5
Dividing large numbers by 5 is actually very easy. All you need to do is simply multiply by 2 and move the decimal point: 195 / 5
Step1: 195×2 = 390
Step2: Move the comma: 39.0 or just 39.
2978 / 5
Step1: 2978×2 = 5956
Step2: 595.6
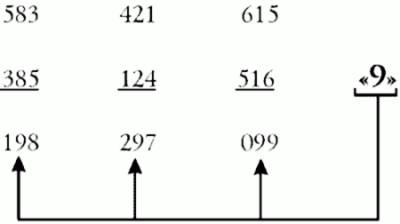
9. Subtraction from 1000
To subtract from 1000, you can use this simple rule: Subtract all digits from 9 except the last one. And subtract the last digit from 10:
1000-648
Step1: subtract 6 from 9 = 3
Step2: subtract 4 = 5 from 9
Step3: subtract 8 from 10 = 2
Answer: 352
And finally, a few mathematical tricks:
Interesting results:
1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 + 10 = 1111111111
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
Favorite number.
Offer to think of your favorite number. Now multiply (on a calculator) the number 15873 by your favorite number multiplied by 7. For example, if your favorite number is 5, then you need to multiply by 35. You will get a product written only with your favorite number.
The second option is also possible: multiply the number 12345679 by your favorite number multiplied by 9, in our case this is the number 45.
The explanation for this trick is quite simple: if you multiply 15873 by 7, you get 111111, and if you multiply 12345679 by 9, you get 111111111.
Guess the age.
We multiply the number of our years by 10, then multiply any single-digit number by 9, subtract the second from the first product and report the resulting difference. In this number, the “magician” must add the units digit with the tens digit to get the number of years.
Always a nine
Invite someone to write a number from three different digits, and underneath it write a number from the same digits, but in reverse order. Then subtract the smaller from the larger. When the spectator does this, tell him that there is a nine in the middle of the number.
The secret of the trick: You will be right, because the nine will always be in the middle no matter what numbers are written.
A math lesson from the distant past
The math problem for mental calculation was taken from a painting by artist N.P. Bogdanov-Belsky “Oral calculation. At the public school of S. A. Rachinsky,” written in 1895 (kept in the Tretyakov State Gallery). The artist, himself a former student of Sergei Alexandrovich Rachinsky, depicted a regular lesson at a school in the village of Tateevo
And here is the problem that peasant children solved in their heads!!!
“The grandfather was asked how old his grandson was. The grandfather answered that the boy lived as many weekdays as his mother lived on Sundays, as many days as his father lived in weeks, and as many months as his grandmother lived in years. All of them without the boy are 100 years old. How old is the boy?
I thought and, in my opinion, for a long time...



